【题目】甲乙两人匀速从学校出发,相约在某景点见面,甲于8:00出发5分钟后,乙以 a米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s与t的关系示意图一部分如图所示.
根据图中提供的信息回答下列问题:
(1)甲行走的速度为______米/分;
(2)补齐图象,并指出甲到达景点的时刻;
(3)求a的值.

参考答案:
【答案】(1)60;(2)补图见解析;甲到达时间为8:50;(3)a=100.
【解析】
(1)由图象得,甲5分钟走了300米,据此可求速度;
(2)根据题意补齐图象,求出甲到达景点所需的时间即可得到到达景点的时刻;
(3)求出学校到景点的距离和乙行走的时间,即可求出a的值.
解:(1)![]() 米/分,
米/分,
故答案为:60;
(2)作图如图,
因为![]() ,15+35=50,
,15+35=50,
所以甲花50分钟到达景点,到达时间为8:50;

(3)因为学校到景点的距离为![]() (米),乙行走的时间为35-5=30(分),
(米),乙行走的时间为35-5=30(分),
所以乙行走的速度为3000÷30=100米/分,即![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知线段
 ,点C为线段AB上的一动点,点D、E分别是AC和BC中点.
,点C为线段AB上的一动点,点D、E分别是AC和BC中点.
 若
若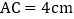 ,求DE的长;
,求DE的长; 试说明无论AC取何值
试说明无论AC取何值 不超过
不超过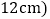 ,DE的长不变;
,DE的长不变;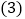 如图2,已知
如图2,已知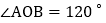 ,过角的内部一点C画射线OC,若OD、OE分别平分
,过角的内部一点C画射线OC,若OD、OE分别平分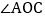 和
和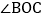 ,试说明
,试说明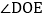 的度数与射线OC的位置无关.
的度数与射线OC的位置无关. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC,∠ACB=90°,∠B=2∠A.
(1)用直尺和圆规作△ABC的角平分线BD,保留作图痕迹;
(2)在(1)的基础上,求∠ADB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个三位正整数t,将各数位上的数字重新排序后(包括本身),得到一个新的三位数
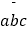 (a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的
(a≤c),在所有重新排列的三位数中,当|a+c﹣2b|最小时,称此时的 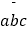 为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
为t的“最优组合”,并规定F(t)=|a﹣b|﹣|b﹣c|,例如:124重新排序后为:142、214、因为|1+4﹣4|=1,|1+2﹣8|=5,|2+4﹣2|=4,所以124为124的“最优组合”,此时F(124)=﹣1.
(1)三位正整数t中,有一个数位上的数字是另外两数位上的数字的平均数,求证:F(t)=0
(2)一个正整数,由N个数字组成,若从左向右它的第一位数能被1整除,它的前两位数能被2整除,前三位数能被3整除,…,一直到前N位数能被N整除,我们称这样的数为“善雅数”.例如:123的第一位数1能披1整除,它的前两位数12能被2整除,前三位数123能被3整除,则123是一个“善雅数”.若三位“善雅数”m=200+10x+y(0≤x≤9,0≤y≤9,x、y为整数),m的各位数字之和为一个完全平方数,求出所有符合条件的“善雅数”中F(m)的最大值. -
科目: 来源: 题型:
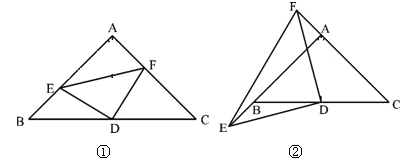
查看答案和解析>>【题目】已知:三角形ABC中,∠A=90°,AB=AC,D为BC的中点,
(1)如图①,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.
(2)如图②,若E,F分别为AB,CA延长线上的点,仍有BE=AF,其他条件不变,那么△DEF是否仍为等腰直角三角形?证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学学生步行到郊外旅行,七年级
 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米 小时,七
小时,七 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米 小时.
小时.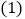 后队追上前队需要多长时间?
后队追上前队需要多长时间?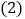 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少? 七年级
七年级 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米? -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:
在上学期的学习中,我们知道若
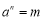 ,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于
,其中a是底数,n是指数,m称为幂,知道a和n可以求m.我们不妨思考:如果知道a,m,能否求n呢?对于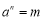 ,规定[a,m]=n,例如:
,规定[a,m]=n,例如: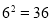 ,所以[6,36]=2.
,所以[6,36]=2.(1)根据上述规定,填空:[3,______]= 4,[2,32]=_____,[-4,1]=______,[5,0.2]=______;
(2)记
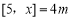 ,
, ,求y与x之间的关系式.
,求y与x之间的关系式.
相关试题

