【题目】如图,海中有一小岛P,在距小岛P的![]() 海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?
海里范围内有暗礁,一轮船自西向东航行,它在A处时测得小岛P位于北偏东60°,且A、P之间的距离为32海里,若轮船继续向正东方向航行,轮船有无触礁危险?请通过计算加以说明.如果有危险,轮船自A处开始至少沿东偏南多少度方向航行,才能安全通过这一海域?

参考答案:
【答案】轮船自A处开始至少沿南偏东75°度方向航行,才能安全通过这一海域.
【解析】
试题分析: 过P作PB⊥AM于B,则PC的长是A沿AM方向距离P点的最短距离,求出PC长和16![]() 比较即可,第二问设出航行方向,利用特殊角的三角函数值确定答案.
比较即可,第二问设出航行方向,利用特殊角的三角函数值确定答案.
试题解析:过P作PB⊥AM于B,
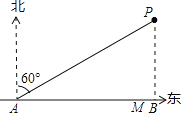
在Rt△APB中,∵∠PAB=30°,
∴PB=![]() AP=
AP=![]() ×32=16海里,
×32=16海里,
∵16<16![]() 故轮船有触礁危险,
故轮船有触礁危险,
为了安全,应该变航行方向,并且保证点P到航线的距离不小于暗礁的半径16![]() 海里,即这个距离至少为16
海里,即这个距离至少为16![]() 海里,
海里,
设安全航向为AC,作PD⊥AC于点D,
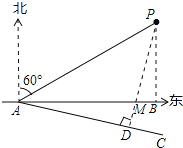
由题意得,AP=32海里,PD=16![]() 海里,
海里,
∵sin∠PAC=![]() ,
,
∴在Rt△PAD中,∠PAC=45°,
∴∠BAC=∠PAC-∠PAB=45°-30°=15°,
答:轮船自A处开始至少沿东偏南15°度方向航行,才能安全通过这一海域.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC≌Rt△CED,点B、C、E在同一直线上,则结论:①AC=CD,②AC⊥CD,③BE=AB+DE,④AB∥ED,其中成立的有( )

A. 仅① B. 仅①③ C. 仅①③④ D. ①②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线y=
 x与双曲线y=
x与双曲线y= 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为 .
.(1)求k的值;
(2)若双曲线y=
 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=
 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小学开展4种课外兴趣小组活动,分别为A;绘画:B;机器人:C;跳舞:D;吉他.每个学生都要选取一个兴趣小组参与活动,小明对同学们选取的活动形式进行了随机抽样调查,根据调查统计结果,绘制了如下的统计图:

(1)本次调查学生共 人,a= ,并将条形图补充完整;
(2)如果该校有学生500人,则选择“机器人”活动的学生估计有多少人?
(3)学校让每班同学在A,B,C,D四种活动形式中,随机抽取两种开展活动,请用树状图或列表法的方法,求每班抽取的两种形式恰好是“绘画”和“机器人”的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将图1,将一张直角三角形纸片ABC折叠,使点A与点C重合,这时DE为折痕,△CBE为等腰三角形;再继续将纸片沿△CBE的对称轴EF折叠,这时得到了两个完全重合的矩形(其中一个是原直角三角形的内接矩形,另一个是拼合成的无缝隙、无重叠的矩形),我们称这样两个矩形为“叠加矩形”.

(1)如图2,正方形网格中的△ABC能折叠成“叠加矩形”吗?如果能,请在图2中画出折痕;
(2)如图3,在正方形网格中,以给定的BC为一边,画出一个斜三角形ABC,使其顶点A在格点上,且△ABC折成的“叠加矩形”为正方形;
(3)如果一个三角形所折成的“叠加矩形”为正方形,那么它必须满足的条件是 ;
(4)如果一个四边形一定能折成“叠加矩形”,那么它必须满足的条件是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC的平分线,∠EAD=10°,∠B=50°,求∠C的度数.
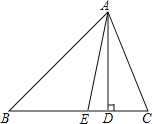
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,点E为CD的中点,连接AE延长交BC的延长线于点F,连接BE,AE=FE,BE⊥AF.
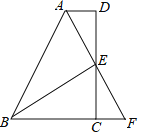
(1)求证:△AED≌△FEC
(2)求证:AB=BC+AD
相关试题

