搜索
【题目】如图，在四边形ABCD中，点E为CD的中点，连接AE延长交BC的延长线于点F，连接BE，AE＝FE，BE⊥AF．
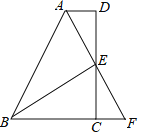
（1）求证：△AED≌△FEC
（2）求证：AB＝BC＋AD
参考答案：
【答案】（1）见解析；（2）见解析
【解析】
（1）先利用中点证明DE=CE，再用SAS证明△AED≌△FEC即可；
（2）由AE=FE， BE⊥AF可知BE垂直平分AF，则有AB=FB，利用全等可得出AD=FC，则结论可证．
证明：（1）∵点E为CD的中点
∴DE=CE
在△AED与△FEC中，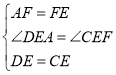
∴△AED≌△FEC（SAS）
（2）∵AE=FE， BE⊥AF
∴BE垂直平分AF
∴AB=FB
由（1）得：△AED≌△FEC
∴AD=FC
∴AB=FB =BC+FC =BC+AD
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，海中有一小岛P，在距小岛P的
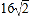海里范围内有暗礁，一轮船自西向东航行，它在A处时测得小岛P位于北偏东60°，且A、P之间的距离为32海里，若轮船继续向正东方向航行，轮船有无触礁危险？请通过计算加以说明．如果有危险，轮船自A处开始至少沿东偏南多少度方向航行，才能安全通过这一海域？
-
科目： 来源： 题型：
查看答案和解析>>【题目】将图1，将一张直角三角形纸片ABC折叠，使点A与点C重合，这时DE为折痕，△CBE为等腰三角形；再继续将纸片沿△CBE的对称轴EF折叠，这时得到了两个完全重合的矩形（其中一个是原直角三角形的内接矩形，另一个是拼合成的无缝隙、无重叠的矩形），我们称这样两个矩形为“叠加矩形”．
（1）如图2，正方形网格中的△ABC能折叠成“叠加矩形”吗？如果能，请在图2中画出折痕；
（2）如图3，在正方形网格中，以给定的BC为一边，画出一个斜三角形ABC，使其顶点A在格点上，且△ABC折成的“叠加矩形”为正方形；
（3）如果一个三角形所折成的“叠加矩形”为正方形，那么它必须满足的条件是 ；
（4）如果一个四边形一定能折成“叠加矩形”，那么它必须满足的条件是 ．
-
科目： 来源： 题型：
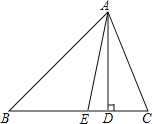
查看答案和解析>>【题目】如图，在△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠EAD＝10°，∠B＝50°，求∠C的度数．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，∠A＝60°，点D是BC边的中点，DE⊥BC，∠ABC的平分线BF交DE于△ABC内一点P，连接PC．
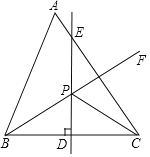
（1）若∠ABP＝32°，求∠ACP的度数；
（2）若∠ACP＝m°，∠ABP＝n°，请直接写出m，n满足的关系式：________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，平面直角坐标系中，点A、B、C在x轴上，点D、E在y轴上，OA=OD=2，OC=OE=4，B为线段OA的中点，直线AD与经过B、E、C三点的抛物线交于F、G两点，与其对称轴交于M，点P为线段FG上一个动点（与F、G不重合），PQ∥y轴与抛物线交于点Q．
（1）求经过B、E、C三点的抛物线的解析式；
（2）判断△BDC的形状，并给出证明；当P在什么位置时，以P、O、C为顶点的三角形是等腰三角形，并求出此时点P的坐标；
（3）若抛物线的顶点为N，连接QN，探究四边形PMNQ的形状：①能否成为菱形；②能否成为等腰梯形？若能，请直接写出点P的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店经销一种成本为每千克
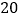元的水产品，据市场分析，若按每千克
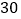元销售，一个月能售出
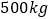，销售单价每涨（或跌）
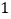元，月销售量就减少（或增加）
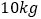，解答以下问题：（1）当销售单价定位每千克
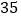元时，计算月销售量和月销售利润；（2）商店想在月销售成本不超过
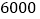元的情况下，使得月销售利润达到
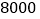元，销售单价应为多少？（3）商店要使得月销售利润达到最大，销售单价应为多少？此时利润为多少？
相关试题
