【题目】如图,已知直线y=![]() x与双曲线y=
x与双曲线y=![]() 交于A、B两点,且点A的横坐标为
交于A、B两点,且点A的横坐标为![]() .
.
(1)求k的值;
(2)若双曲线y=![]() 上点C的纵坐标为3,求△AOC的面积;
上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=![]() 上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.
上有一点N,若以O、M、P、N为顶点的四边形是有一组对角为60°的菱形,请写出所有满足条件的点P的坐标.

参考答案:
【答案】(1)k=![]() (2)
(2)![]() (3)(1,
(3)(1,![]() )或(﹣1,﹣
)或(﹣1,﹣![]() );(3,
);(3,![]() )或(﹣3,﹣
)或(﹣3,﹣![]() )
)
【解析】
(1)先求的A点纵坐标,然后用待定系数法求解即可;
(2)先求出C点坐标,再用待定系数法求的直线AC的解析式,然后求得直线AC与x的交点坐标,再根据![]() 求解即可;
求解即可;
(3)设![]() 点坐标
点坐标![]() ,根据题意用关于a的式子表示出N的坐标,再根据菱形的性质得
,根据题意用关于a的式子表示出N的坐标,再根据菱形的性质得![]() ,求出a的值即可.
,求出a的值即可.
![]() 把x=
把x=![]() 代入
代入![]() ,得y=
,得y=![]() ,
,
∴A(![]() ,1),
,1),
把点![]() 代入
代入![]() ,解得:
,解得:![]() ;
;
![]() ∵把y=3代入函数
∵把y=3代入函数![]() ,得x=
,得x=![]() ,
,
∴C![]() ,
,
设过![]() ,
,![]() 两点的直线方程为:
两点的直线方程为:![]() ,
,
把点![]() ,
,![]() ,代入得:
,代入得:
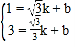 ,
,
解得:![]() ,
,
∴![]() ,
,
设![]() 与
与![]() 轴交点为
轴交点为![]() ,
,
则![]() 点坐标为
点坐标为![]() ,
,
∴![]() ;
;
![]() 设
设![]() 点坐标
点坐标![]() ,由直线
,由直线![]() 解析式可知,直线
解析式可知,直线![]() 与
与![]() 轴正半轴夹角为
轴正半轴夹角为![]() ,
,
∵以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是有一组对角为
为顶点的四边形是有一组对角为![]() 的菱形,
的菱形,![]() 在直线
在直线![]() 上,
上,
∴点![]() 只能在
只能在![]() 轴上,
轴上,
∴![]() 点的横坐标为
点的横坐标为![]() ,代入
,代入![]() ,解得纵坐标为:
,解得纵坐标为:![]() ,
,
根据![]() ,即得:
,即得:![]() ,
,
解得:![]() .
.
故![]() 点坐标为:
点坐标为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题探究)
将三角形
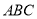 纸片沿
纸片沿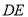 折叠,使点A落在点
折叠,使点A落在点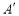 处.
处.(1)如图,当点A落在四边形
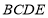 的边
的边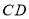 上时,直接写出
上时,直接写出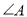 与
与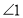 之间的数量关系;
之间的数量关系;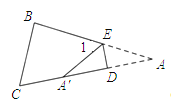
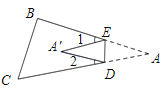
(2)如图,当点A落在四边形
 的内部时,求证:
的内部时,求证: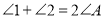 ;
;
(3)如图,当点A落在四边形
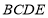 的外部时,探索
的外部时,探索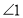 ,
,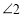 ,
,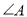 之间的数量关系,并加以证明;
之间的数量关系,并加以证明;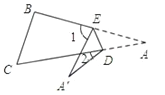
(拓展延伸)
(4)如图,若把四边形
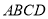 纸片沿
纸片沿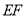 折叠,使点A、D落在四边形
折叠,使点A、D落在四边形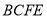 的内部点
的内部点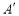 、
、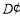 的位置,请你探索此时
的位置,请你探索此时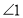 ,
,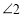 ,
,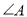 ,
,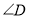 之间的数量关系,写出你发现的结论,并说明理由.
之间的数量关系,写出你发现的结论,并说明理由.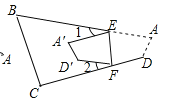
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形
 的边长为
的边长为 ,点
,点 为
为 上的一点,点
上的一点,点 为
为 上的一点,连结
上的一点,连结 、
、 ,
, .
.
 求证:①
求证:① ;②
;② ;
; 若
若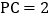 ,求
,求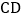 和
和 的长.
的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了预防“流感”,某学校对教室采用药熏消毒法进行消毒,已知药物燃烧时,室内每立方米空气中的含药量
 与时间
与时间 成正比例,药物燃烧完后,
成正比例,药物燃烧完后, 与
与 成反比例(如图所示).现测得药物
成反比例(如图所示).现测得药物 燃毕,此时室内空气中每立方米的含药量为
燃毕,此时室内空气中每立方米的含药量为 .研究表明,当空气中每立方米的含药量不低于
.研究表明,当空气中每立方米的含药量不低于 才有效,那么此次消毒的有效时间是( )
才有效,那么此次消毒的有效时间是( )
A.
 分钟 B.
分钟 B.  分钟 C.
分钟 C.  分钟 D.
分钟 D.  分钟
分钟 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知直线
 过
过 与
与 交于
交于 点、
点、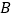 点,与
点,与 交于
交于 点,直线
点,直线 与
与 轴交于
轴交于 点,且
点,且 ,则
,则 ________.
________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知AB=AC.如图,D、E为∠BAC的平分线上的两点,连接BD、CD、BE、CE;如图4, D、E、F为∠BAC的平分线上的三点,连接BD、CD、BE、CE、BF、CF;如图5, D、E、F、G为∠BAC的平分线上的四点,连接BD、CD、BE、CE、BF、CF、BG、CG……依此规律,第17个图形中有全等三角形的对数是( )

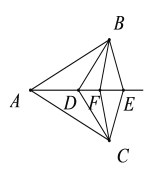

A.17B.54C.153D.171
-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
 (a>0,a为常数)和y=
(a>0,a为常数)和y= 在第一象限内的图象如图所示,点M在y=
在第一象限内的图象如图所示,点M在y= 的图象上,MC⊥x轴于点C,交y=
的图象上,MC⊥x轴于点C,交y= 图象于点A;MD⊥y轴于点D,交y=
图象于点A;MD⊥y轴于点D,交y= 的图象于点B,当点M在y=
的图象于点B,当点M在y= 的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;
的图象上运动时,以下结论:①S△ODB=S△OCA;②四边形OAMB的面积不变;③当点A是MC的中点时,则点B是MD的中点.其中正确结论的序号是___________;
相关试题

