【题目】如图,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE.连接DE、DF、EF. 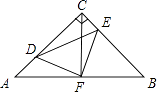
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
参考答案:
【答案】
(1)证明:在等腰直角△ABC中,∠ACB=90°,AC=BC,
∴∠A=∠B=45°,
又∵F是AB中点,
∴∠ACF=∠FCB=45°,
即,∠A=∠FCE=∠ACF=45°,且AF=CF,
在△ADF与△CEF中, 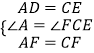 ,
,
∴△ADF≌△CEF(SAS)
(2)证明:由(1)可知△ADF≌△CEF,
∴DF=FE,
∴△DFE是等腰三角形,
又∵∠AFD=∠CFE,
∴∠AFD+∠DFC=∠CFE+∠DFC,
∴∠AFC=∠DFE,
∵∠AFC=90°,
∴∠DFE=90°,
∴△DFE是等腰直角三角形
【解析】(1)根据在等腰直角△ABC中,∠ACB=90°,AC=BC,利用F是AB中点,∠A=∠FCE=∠ACF=45°,即可证明:△ADF≌△CEF.(2)利用△ADF≌△CEF,∠AFD+∠DFC=∠CFE+∠DFC,和∠AFC=90°即可证明△DFE是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件是必然事件的是( )
A.任意购买一张电影票,座号是“7排8号”B.射击运动员射击一次,恰好命中靶心
C.抛掷一枚图钉,钉尖触地D.13名同学中,至少2人出生的月份相同
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一元一次方程的解是一元一次不等式组的解,那么称该一元一次方程为该不等式组的关联方程.
(1)若不等式组
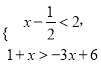 的一个关联方程的解是整数,则这个关联方程可以是 (写出一个即可);
的一个关联方程的解是整数,则这个关联方程可以是 (写出一个即可);(2)若方程3-x=2x,3+x=2(x+
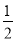 )都是关于
)都是关于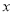 的不等式组
的不等式组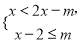 的关联方程,试求
的关联方程,试求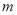 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】请观察图形,并探究和解决下列问题:
(1)在第n个图形中,每一横行共有 个正方形,每一竖列共有 个正方形;
(2)在铺设第n个图形时,共有 个正方形;
(3)某工人需用黑白两种木板按图铺设地面,如果每块黑板成本为8元,每块白木板成本6元,铺设当n=5的图形时,共需花多少钱购买木板?

-
科目: 来源: 题型:
查看答案和解析>>【题目】三角形ABC的三条内角平分线为AE,BF,CG,下面的说法中正确的个数有( )
①△ABC的内角平分线上的点到三边距离相等
②三角形的三条内角平分线交于一点
③三角形的内角平分线位于三角形的内部
④三角形的任一内角平分线将三角形分成面积相等的两部分.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】一件商品按成本价提高20%后标价,又以9折销售,售价为270元.这种商品的成本价是多少?
-
科目: 来源: 题型:
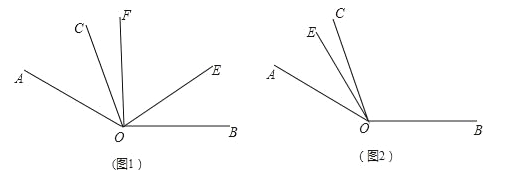
查看答案和解析>>【题目】如图1,已知∠AOB=140°,∠AOC=30°,OE是∠AOB内部的一条射线,且OF平分∠AOE.
(1)若∠EOB=30°,则∠COF= ;
(2)若∠COF=20°,则∠EOB= ;
(3)若∠COF=n°,则∠EOB= (用含n的式子表示).
(4)当射线OE绕点O逆时针旋转到如图2的位置时,请把图补充完整;此时,∠COF与∠EOB有怎样的数量关系?请说明理由.
相关试题

