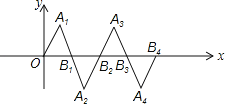
【题目】在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是 .
参考答案:
【答案】(4n+1,![]() )
)
【解析】
试题分析:首先根据△OA1B1是边长为2的等边三角形,可得A1的坐标为(1,![]() ),B1的坐标为(2,0);然后根据中心对称的性质,分别求出点A2、A3、A4的坐标各是多少;最后总结出An的坐标的规律,求出A2n+1的坐标是多少即可.
),B1的坐标为(2,0);然后根据中心对称的性质,分别求出点A2、A3、A4的坐标各是多少;最后总结出An的坐标的规律,求出A2n+1的坐标是多少即可.
解:∵△OA1B1是边长为2的等边三角形,
∴A1的坐标为(1,![]() ),B1的坐标为(2,0),
),B1的坐标为(2,0),
∵△B2A2B1与△OA1B1关于点B1成中心对称,
∴点A2与点A1关于点B1成中心对称,
∵2×2﹣1=3,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A2的坐标是(3,﹣![]() ),
),
∵△B2A3B3与△B2A2B1关于点B2成中心对称,
∴点A3与点A2关于点B2成中心对称,
∵2×4﹣3=5,2×0﹣(﹣![]() )=
)=![]() ,
,
∴点A3的坐标是(5,![]() ),
),
∵△B3A4B4与△B3A3B2关于点B3成中心对称,
∴点A4与点A3关于点B3成中心对称,
∵2×6﹣5=7,2×0﹣![]() =﹣
=﹣![]() ,
,
∴点A4的坐标是(7,﹣![]() ),
),
…,
∵1=2×1﹣1,3=2×2﹣1,5=2×3﹣1,7=2×3﹣1,…,
∴An的横坐标是2n﹣1,A2n+1的横坐标是2(2n+1)﹣1=4n+1,
∵当n为奇数时,An的纵坐标是![]() ,当n为偶数时,An的纵坐标是﹣
,当n为偶数时,An的纵坐标是﹣![]() ,
,
∴顶点A2n+1的纵坐标是![]() ,
,
∴△B2nA2n+1B2n+1(n是正整数)的顶点A2n+1的坐标是(4n+1,![]() ).
).
故答案为:(4n+1,![]() ).
).
-
科目: 来源: 题型:
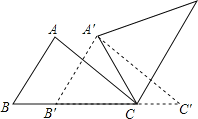
查看答案和解析>>【题目】如图,△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A′B′C′,再将△A′B′C′绕点A′逆时针旋转一定角度后,点B′恰好与点C重合,则平移的距离为 ,旋转角的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程ax2+2x﹣5=0的两根中有且仅有一根在0和1之间(不含0和1),则a的取值范围是( )
A.a<3 B.a>3 C.a<﹣3 D.a>﹣3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,E、F分别是BC、CD上的两个动点,且AE⊥EF.则AF的最小值是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等边△ABC中,点D在直线BC上,连接AD,作∠ADN=60°,直线DN交射线AB于点E,过点C作CF∥AB交直线DN于点F.

(1)当点D在线段BC上,∠NDB为锐角时,如图①,
①判断∠1与∠2的大小关系,并说明理由;
②过点F作FM∥BC交射线AB于点M,求证:CF+BE=CD;
(2)当点D在线段BC的延长线上,∠NDB为锐角时,如图②;
当点D在线段CB的延长线上,∠NDB为钝角时,如图③;
请分别写出线段CF,BE,CD之间的数量关系,不需要证明;
(3)在(2)的条件下,若∠ADC=30°,S△ABC=4
 ,直接写出BE和CD的长度.
,直接写出BE和CD的长度. -
科目: 来源: 题型:
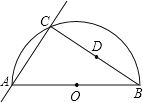
查看答案和解析>>【题目】如图,AB是半圆O的直径,AB=10,过点A的直线交半圆于点C,且AC=6,连结BC,点D为BC的中点.已知点E在直线AC上,△CDE与△ACB相似,则线段AE的长为 3或 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是
A.a6÷a2=a3 B.3a2b﹣a2b=2 C.(﹣2a3)2=4a6 D.(a+b)2=a2+b2
相关试题

