【题目】阅读下面材料
在数轴上4与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]()
在数轴上![]() 与3所对的两点之间的距离
与3所对的两点之间的距离![]() ;
;
在数轴上![]() 与
与![]() 所对的两点之间的距离:
所对的两点之间的距离:![]() 在数轴上点A、B分别表示数a、b,则A、B两点之间的距离
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离![]()
依据材料知识解答下列问题
![]() 数轴上表示
数轴上表示![]() 和
和![]() 的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
![]() 七年级研究性学习小组进行如下探究:
七年级研究性学习小组进行如下探究:
![]() 请你在草稿纸上面出数轴当表示数x的点在
请你在草稿纸上面出数轴当表示数x的点在![]() 与2之间移动时,
与2之间移动时,![]() 的值总是一个固定的值为:______,式子
的值总是一个固定的值为:______,式子![]() 的最小值是______.
的最小值是______.
![]() 请你在草稿纸上画出数轴,当x等于______时,
请你在草稿纸上画出数轴,当x等于______时,![]() 的值最小,且最小值是______.
的值最小,且最小值是______.
参考答案:
【答案】(1)2,![]() 或
或![]() (2)①5,1②2,7
(2)①5,1②2,7
【解析】
![]() 根据数轴上A、B两点之间的距离
根据数轴上A、B两点之间的距离![]() 的表达式计算出绝对值;
的表达式计算出绝对值;
![]() 要去掉绝对值符号,需要抓住已知点在数轴上进行分段讨论,写出去绝对值后的表达式讨论计算即可.
要去掉绝对值符号,需要抓住已知点在数轴上进行分段讨论,写出去绝对值后的表达式讨论计算即可.
![]() 根据题意知
根据题意知![]() 和
和![]() 的两点之间的距离可表示为:
的两点之间的距离可表示为:![]() ;数x和3的两点之间的距离
;数x和3的两点之间的距离![]() 或
或![]() ;
;
故答案为2,![]() 或
或![]() ;
;
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
所以当![]() 时,
时,![]() 的值总是一个固定的值为5.
的值总是一个固定的值为5.
![]() 是表示x到A、C的距离之和,可观察下图.
是表示x到A、C的距离之和,可观察下图.
当![]() 时,由
时,由![]() 可知
可知![]()
当![]() 时,
时,![]()
![]() 当
当![]() 时,式子
时,式子![]() 的最小值是1.
的最小值是1.
故答案为5,1.
![]() 画出图形,则可知,
画出图形,则可知,![]() 是表示x的点到A、B、C三点距离之和
是表示x的点到A、B、C三点距离之和
分区间来讨论,可以得出
当![]() 时,
时,![]() ,可见
,可见![]() 取得最小值,
取得最小值,![]() ;
;
当![]() 时,
时,![]() ,
,![]() 时取得最小值,
时取得最小值,![]() .
.
所以式![]() 当x等于2时,最小值是7.
当x等于2时,最小值是7.
故答案为2,7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,
(1)求证:AE=CE;
(2)求证:四边形ABDF是平行四边形;
(3)若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点
 是线段
是线段 上的动点(点
上的动点(点 与
与 不重合),分别以
不重合),分别以 为边向线段
为边向线段 的同一侧作正
的同一侧作正 和正
和正 .
.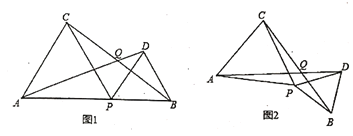
(1)请你判断
 与
与 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;(2)连接
 ,相交于点
,相交于点 ,设
,设 ,那么
,那么 的大小是否会随点
的大小是否会随点 的移动而变化?请说明理由;
的移动而变化?请说明理由;(3)如图2,若点
 固定,将
固定,将 绕点
绕点 按顺时针方向旋转(旋转角小于
按顺时针方向旋转(旋转角小于 ),此时
),此时 的大小是否发生变化?(只需直接写出你的猜想,不必证明)
的大小是否发生变化?(只需直接写出你的猜想,不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】说明:从(A),(B)两题中任选一题做答.
春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售20件;如果每件降价1元,那么每天能多售出40件.
(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件定价多少元?
我选择:
-
科目: 来源: 题型:
查看答案和解析>>【题目】说明:在解答“结论应用”时,从(A),(B)两题中仸选一题做答.
问题探究
启知学习小组在课外学习时,发现了这样一个问题:如图(1),在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图(1)中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
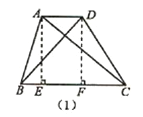
结论应用
在平面直角坐标系中,反比例函数
 的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.(A)(1)求反比例函数的表达式;
(2)如图(2),已知b=1,AC,BD相交于点E,求证:CD∥AB.
(B)(1)求反比例函数的表达式;
(2)如图(3),若点B在第三象限,判断并证明CD与AB的位置关系.
我选择:


-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x2+4x-5=0;(2)x(x-4)=2-8x;(3)x-3=4(x-3)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程3x2-(a-3)x-a=0(a>0).
(1)求证:方程总有两个不相等的实数根;
(2)若方程有一个根大于2,求a的取值范围.
相关试题

