【题目】说明:在解答“结论应用”时,从(A),(B)两题中仸选一题做答.
问题探究
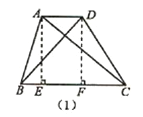
启知学习小组在课外学习时,发现了这样一个问题:如图(1),在四边形ABCD中,连接AC,BD,如果△ABC与△BCD的面积相等,那么AD∥BC.在小组交流时,他们在图(1)中添加了如图所示的辅助线,AE⊥BC于点E,DF⊥BC于点F.请你完成他们的证明过程.
结论应用
在平面直角坐标系中,反比例函数![]() 的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
的图象经过A(1,4),B(a,b)两点,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
(A)(1)求反比例函数的表达式;
(2)如图(2),已知b=1,AC,BD相交于点E,求证:CD∥AB.
(B)(1)求反比例函数的表达式;
(2)如图(3),若点B在第三象限,判断并证明CD与AB的位置关系.
我选择:


参考答案:
【答案】问题探究:证明见解析证明;结论应用:若选(A)(1)![]() ;(2)见解析证明;若选(B)(1)
;(2)见解析证明;若选(B)(1)![]() ;(2)CD∥AB,见解析证明.
;(2)CD∥AB,见解析证明.
【解析】
试题分析:问题探究:根据![]()
![]() ,可得AE=DF,根据AE⊥BC,DF⊥BC,得AE∥DF,所以可判定四边形AEFD是平行四边形,即可得出结论;
,可得AE=DF,根据AE⊥BC,DF⊥BC,得AE∥DF,所以可判定四边形AEFD是平行四边形,即可得出结论;
结论应用:若选(A)(1)把A点的坐标代入解析式即可求出m的值即可;(2)连接AD、BC,将b=1代入函数表达式得a=4,由C、D、E三点的坐标可知CE=DE=1,AE=BE=3,进而可得![]()
![]() ,即可得出结论;
,即可得出结论;
若选(B)(1)把A点的坐标代入解析式中即可求出m的值即可;(2)连接AD、BC,延长BD,AC相交于点M,由题意得M点坐标为(1,b),BM=1-a,AM=4-b,且![]() ,通过计算可得出
,通过计算可得出![]()
![]() ,即可得出结论.
,即可得出结论.
试题解析:问题探究:∵![]() ,
,![]() ,∵
,∵![]()
![]() ,∴AE=DF,又∵AE⊥BC,DF⊥BC,∴AE∥DF,∴四边形AEFD是平行四边形,∴AD∥BC;
,∴AE=DF,又∵AE⊥BC,DF⊥BC,∴AE∥DF,∴四边形AEFD是平行四边形,∴AD∥BC;
结论应用:若选(A)(1)把A点的坐标代入解析式中得:4=![]() ,m=4,∴反比例函数的表达式为:
,m=4,∴反比例函数的表达式为:![]() ;
;
(2)连接AD、BC,将b=1代入函数表达式得:a=4,又∵AC⊥x,BD⊥y,∴AC⊥BD,C(1,0),D(0,1),E(1,1),∴CE=DE=1,AE=BE=3,又∵![]() ,∴
,∴![]() 且AC=BD=4,BE=AE=3,∴
且AC=BD=4,BE=AE=3,∴![]()
![]() ,∴CD∥AB;
,∴CD∥AB;

若选(B)(1)把A点的坐标代入解析式中得:4=![]() ,m=4,∴反比例函数的表达式为:
,m=4,∴反比例函数的表达式为:![]() ;
;
(2)CD∥AB,证明如下:连接AD、BC,延长BD,AC相交于点M,由题意得M点坐标为(1,b),BM=1-a,AM=4-b,且![]() ,∴
,∴![]() =
=![]() ×4(1-a)=2(1-a),
×4(1-a)=2(1-a),![]() =
=![]() (-a)(4-b)=
(-a)(4-b)=![]() (-a)(4-
(-a)(4-![]() )=2(1-a),∴
)=2(1-a),∴![]()
![]() ,∴CD∥AB.
,∴CD∥AB.

-
科目: 来源: 题型:
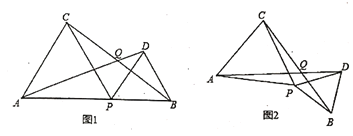
查看答案和解析>>【题目】如图1,点
 是线段
是线段 上的动点(点
上的动点(点 与
与 不重合),分别以
不重合),分别以 为边向线段
为边向线段 的同一侧作正
的同一侧作正 和正
和正 .
.
(1)请你判断
 与
与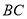 有怎样的数量关系?请说明理由;
有怎样的数量关系?请说明理由;(2)连接
 ,相交于点
,相交于点 ,设
,设 ,那么
,那么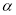 的大小是否会随点
的大小是否会随点 的移动而变化?请说明理由;
的移动而变化?请说明理由;(3)如图2,若点
 固定,将
固定,将 绕点
绕点 按顺时针方向旋转(旋转角小于
按顺时针方向旋转(旋转角小于 ),此时
),此时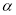 的大小是否发生变化?(只需直接写出你的猜想,不必证明)
的大小是否发生变化?(只需直接写出你的猜想,不必证明) -
科目: 来源: 题型:
查看答案和解析>>【题目】说明:从(A),(B)两题中任选一题做答.
春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售20件;如果每件降价1元,那么每天能多售出40件.
(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件定价多少元?
我选择:
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料
在数轴上4与
 所对的两点之间的距离:
所对的两点之间的距离:
在数轴上
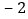 与3所对的两点之间的距离
与3所对的两点之间的距离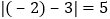 ;
;在数轴上
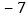 与
与 所对的两点之间的距离:
所对的两点之间的距离: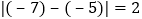 在数轴上点A、B分别表示数a、b,则A、B两点之间的距离
在数轴上点A、B分别表示数a、b,则A、B两点之间的距离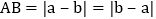
依据材料知识解答下列问题
 数轴上表示
数轴上表示 和
和 的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______;
的两点之间的距离是______,数轴上表示数x和3的两点之间的距离表示为______; 七年级研究性学习小组进行如下探究:
七年级研究性学习小组进行如下探究: 请你在草稿纸上面出数轴当表示数x的点在
请你在草稿纸上面出数轴当表示数x的点在 与2之间移动时,
与2之间移动时,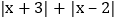 的值总是一个固定的值为:______,式子
的值总是一个固定的值为:______,式子 的最小值是______.
的最小值是______. 请你在草稿纸上画出数轴,当x等于______时,
请你在草稿纸上画出数轴,当x等于______时,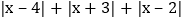 的值最小,且最小值是______.
的值最小,且最小值是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)x2+4x-5=0;(2)x(x-4)=2-8x;(3)x-3=4(x-3)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程3x2-(a-3)x-a=0(a>0).
(1)求证:方程总有两个不相等的实数根;
(2)若方程有一个根大于2,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】青海新闻网讯:2016年2月21日,西宁市首条绿道免费公共自行车租赁系统正式启用.市政府今年投资了112万元,建成40个公共自行车站点、配置720辆公共自行车.今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2018年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)请问每个站点的造价和公共自行车的单价分别是多少万元?
(2)请你求出2016年到2018年市政府配置公共自行车数量的年平均增长率.
相关试题

