【题目】说明:从(A),(B)两题中任选一题做答.
春节前夕,便民超市把一批进价为每件12元的商品,以每件定价20元销售,每天能售出240件.销售一段时间后发现:如果每件涨价1元,那么每天就少售20件;如果每件降价1元,那么每天能多售出40件.
(A)在降价的情况下,要使该商品每天的销售盈利为1800元,每件应降价多少元?
(B)为了使该商品每天销售盈利为1980元,每件定价多少元?
我选择:
参考答案:
【答案】若选(A)3元;若选(B)21元或23元.
【解析】
试题分析:若选(A)设每件商品应降价x元,根据“(20-x-进价)(每天售出的数量+40x)=每天利润,”列出方程求解即可;若选(B)①设每件商品应降价x元,根据“(20-x-进价)(每天售出的数量+40x)=每天利润,”列出方程,此时方程无实数根;②设每件应涨价y元,根据“(20+y-进价)(每天售出的数量-20y)=每天利润,”列出方程求解即可.
试题解析:若选(A)设每件商品应降价x元,根据题意得(20-x-12)(240+40x)=1800,解得![]() ,
,![]() (不符合题意,舍去),答:每件商品应降价3元;
(不符合题意,舍去),答:每件商品应降价3元;
若选(B)①设每件商品应降价x元,根据题意得(20-x-12)(240+40x)=1980,∵△<0,∴原方程无实数根;
②设每件应涨价y元,根据题意得(20+y-12)(240-20y)=1980,解得![]() ,
,![]() ,∴20+3=23(元),20+1=21(元),答:为了使该商品每天销售盈利为1980元,每件定价21元或23元.
,∴20+3=23(元),20+1=21(元),答:为了使该商品每天销售盈利为1980元,每件定价21元或23元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】圆珠笔每支1. 5元,n支圆珠笔 元;当n=10时,计 元
-
科目: 来源: 题型:
查看答案和解析>>【题目】进入冬季,我市空气质量下降,多次出现雾霾天气.商场根据市民健康需要,代理销售一种防尘口罩,进货价为20元/包,经市场销售发现:销售单价为30元/包时,每周可售出200包,每涨价1元,就少售出5包.若供货厂家规定市场价不得低于30元/包,且商场每周完成不少于150包的销售任务.
(1)试确定周销售量y(包)与售价x(元/包)之间的函数关系式;
(2)试确定商场每周销售这种防尘口罩所获得的利润w(元)与售价x(元/包)之间的函数关系式,并直接写出售价x的范围;
(3)当售价x(元/包)定为多少元时,商场每周销售这种防尘口罩所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
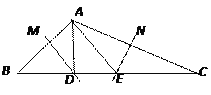
查看答案和解析>>【题目】如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线C1是二次函数y=x2﹣10x在第四象限的一段图象,它与x轴的交点是O、A1;将C1绕点A1旋转180°后得抛物线C2;交x轴于点A2;再将抛物线C2绕A2点旋转180°后得抛物线C3,交x轴于点A3;如此反复进行下去…
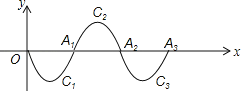
(1)抛物线C3与x轴的交点A3的坐标是多少?抛物线Cn与x轴的交点An的坐标是多少?
(2)若某段抛物线上有一点P(2016,a),试求a的值.
-
科目: 来源: 题型:
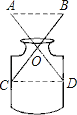
查看答案和解析>>【题目】小红家有一个小口瓶(如图所示),她很想知道它的内径是多少?但是尺子不能伸在里边直接测,于是她想了想,唉!有办法了.她拿来了两根长度相同的细木条,并且把两根长木条的中点固定在一起,木条可以绕中点转动,这样只要量出AB的长,就可以知道玻璃瓶的内径是多少,你知道这是为什么吗?请说明理由.(木条的厚度不计)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的是( )
①点P在∠A的平分线上;
②AS=AR;
③QP∥AR;
④△BRP≌△QSP.
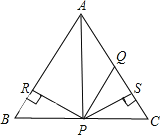
A.全部正确 B.仅①和②正确 C.仅②③正确 D.仅①和③正确
相关试题

