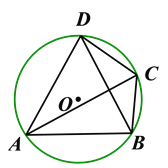
【题目】如图,在⊙O的内接四边形ABCD中,∠BCD=120°,AC平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=6cm,求⊙O的半径.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】【试题分析】(1)因为AC平分∠BCD,∠BCD=120°, 根据角平分线的定义得:∠ACD=∠ACB=60°. 根据同弧所对的圆周角相等,得∠ACD=∠ABD, ∠ACB=∠ADB , ∠ABD=∠ADB=60°.根据三个角是60度的三角形是等边三角形得,△ABD是等边三角形.
(2)作直径DE,连结BE ,由于△ABD是等边三角形,则∠BAD=60°同弧所对的圆周角相等,得∠BED=∠BAD=60°.因为DE是直径,根据直径所对的圆周角是直角得,∠EBD=90°.
则∠EDB=30°,30度所对的直角边是斜边的一半,得DE=2BE .
设EB=x,则ED=2x,根据勾股定理得,(2x)2-x2=62.
解得: ![]() ,即
,即![]() .
.
【试题解析】
(1)∵AC平分∠BCD,∠BCD=120° ,
∴∠ACD=∠ACB=60°.
∵∠ACD=∠ABD, ∠ACB=∠ADB .
∴∠ABD=∠ADB=60°.
∴△ABD是等边三角形.
(2)作直径DE,连结BE
∵△ABD是等边三角形,
∴∠BAD=60°
∴∠BED=∠BAD=60°
∵DE是直径,
∴∠EBD=90°.
∴∠EDB=30°.
∴DE=2BE .
设EB=x,则ED=2x,
∴(2x)2-x2=62.
∵x>0.
∴![]() .
.
∴![]()
即![]() .
.
-
科目: 来源: 题型:
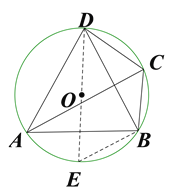
查看答案和解析>>【题目】如图,在△ABC中,∠ABC和∠ACB的平分线BE、CF相交于点P.
(1)若∠ABC=70°,∠ACB=50°,则∠BPC= °;
(2)求证:∠BPC=180°﹣
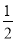 (∠ABC+∠ACB);
(∠ABC+∠ACB);(3)若∠A=α,求∠BPC的度数.

-
科目: 来源: 题型:
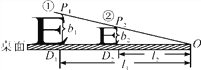
查看答案和解析>>【题目】如图所示,在水平桌面上的两个“E”,当点P1,P2,O在一条直线上时,在点O处用①号“E”测得的视力与用②号“E”测得的视力相同.
(1)图中b1,b2,l1,l2满足怎样的关系式?
(2)若b1=3.2 cm,b2=2 cm,①号“E”的测量距离l1=8 cm,要使测得的视力相同,则②号“E”的测量距离l2应为多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,直线AB∥DC,点P为平面上一点,连接AP与CP.
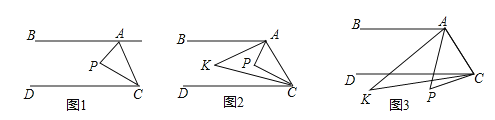
(1)如图1,点P在直线AB、CD之间,当∠BAP=60°,∠DCP=20°时,则∠APC= .
(2)如图2,点P在直线AB、CD之间,∠BAP与∠DCP的角平分线相交于点K,写出∠AKC与∠APC之间的数量关系为 .
(3)如图3,点P落在CD外,∠BAP与∠DCP的角平分线相交于点K,∠AKC与∠APC有何数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(5+i)×(3-4i)=19-17i.
(1)填空:i3= ,i4= .
(2)计算:(3+i)2;
(3)试一试:请利用以前学习的有关知识将
 化简成a+bi的形式
化简成a+bi的形式 -
科目: 来源: 题型:
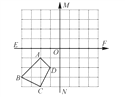
查看答案和解析>>【题目】(齐齐哈尔中考)如图所示,在四边形ABCD中.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称,若对称请在图中画出对称轴或对称中心.
-
科目: 来源: 题型:
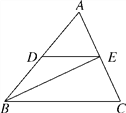
查看答案和解析>>【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.
相关试题

