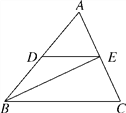
【题目】如图,已知DE∥BC,BE平分∠ABC,∠C=65°,∠ABC=50°.
(1)求∠BED的度数;
(2)判断BE与AC的位置关系,并说明理由.
参考答案:
【答案】(1)25°;(2)BE⊥AC.理由见解析
【解析】试题分析:(1)根据BE平分∠ABC,且∠ABC=50°,可得∠EBC=![]() ∠ABC=25.再根据DE∥BC,即可得出∠BED=∠EBC=25°.
∠ABC=25.再根据DE∥BC,即可得出∠BED=∠EBC=25°.
(2)根据DE∥BC,且∠C=65°,即可得到∠AED=∠C=65°,再根据∠BED=25°,可得∠AEB=∠AED+∠BED=65°+25°=90°,据此可得BE⊥AC.
试题解析:
(1)∵BE平分∠ABC,且∠ABC=50°,
∴∠EBC=![]() ∠ABC=25°.
∠ABC=25°.
∵DE∥BC,
∴∠BED=∠EBC=25°.
(2)BE⊥AC,其理由是:
∵DE∥BC,且∠C=65°,
∴∠AED=∠C=65°.
∵∠BED=25°,
∴∠AEB=∠AED+∠BED=65°+25°=90°,
∴BE⊥AC.
-
科目: 来源: 题型:
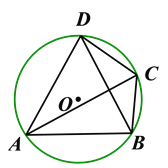
查看答案和解析>>【题目】如图,在⊙O的内接四边形ABCD中,∠BCD=120°,AC平分∠BCD.
(1)求证:△ABD是等边三角形;
(2)若BD=6cm,求⊙O的半径.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
定义:如果一个数的平方等于-1,记为i2=-1,这个数i叫做虚数单位.那么和我们所学的实数对应起来就叫做复数,表示为a+bi(a,b为实数),a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(5+i)×(3-4i)=19-17i.
(1)填空:i3= ,i4= .
(2)计算:(3+i)2;
(3)试一试:请利用以前学习的有关知识将
 化简成a+bi的形式
化简成a+bi的形式 -
科目: 来源: 题型:
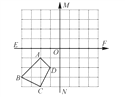
查看答案和解析>>【题目】(齐齐哈尔中考)如图所示,在四边形ABCD中.
(1)画出四边形A1B1C1D1,使四边形A1B1C1D1与四边形ABCD关于直线MN成轴对称;
(2)画出四边形A2B2C2D2,使四边形A2B2C2D2与四边形ABCD关于点O中心对称.
(3)四边形A1B1C1D1与四边形A2B2C2D2是否对称,若对称请在图中画出对称轴或对称中心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分10分)
【感受联系】在初二的数学学习中,我们感受过等腰三角形与直角三角形的密切联系.等腰三角形作底边上的高线可转化为直角三角形,直角三角形沿直角边翻折可得到等腰三角形等等.
【探究发现】某同学运用这一联系,发现了“30°角所对的直角边等于斜边的一半”.并给出了如下的部分探究过程,请你补充完整证明过程
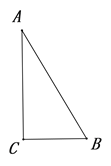
已知:如图,在
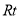 △
△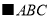 中,
中,  °,
°,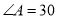 °.
°.求证:
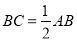 .
.证明:
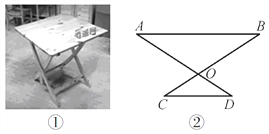
【灵活运用】该同学家有一张折叠方桌如图①所示,方桌的主视图如图②.经测得
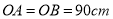 ,
, 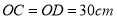 ,将桌子放平,两条桌腿叉开的角度
,将桌子放平,两条桌腿叉开的角度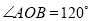 .
.求:桌面与地面的高度.
-
科目: 来源: 题型:
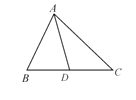
查看答案和解析>>【题目】如图所示,AD是△ABC的边BC的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
-
科目: 来源: 题型:
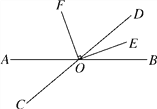
查看答案和解析>>【题目】如图,已知直线AB与CD相交于点O,OE是∠BOD的平分线,OF⊥OE,∠BOE=20°.
(1)求∠AOC的度数;
(2)求∠COF的度数.
相关试题

