【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】
试题(1)甲方案的付款=甲水果单价×购买量,乙方案的付款=乙水果单价×购买量+运输费,根据这两个关系分别列式即可;(2)将甲和乙的两种方案所需的付款数进行比较,从而确定购买量的范围.
解:(1)y甲=9x(x≥3000),y乙=8x+5000(x≥3000);
(2)当y甲=y乙时,即9x=8x+5000,解得x=5000,∴当x=5000千克时,两种付款一样;
当y甲<y乙时,有![]() ,解得3000≤x<5000,∴当3000≤x<5000时,选择甲种方案付款少;
,解得3000≤x<5000,∴当3000≤x<5000时,选择甲种方案付款少;
当y甲>y乙时,有x>5000,∴当x>5000千克时,选择乙种方案付款少.
综上所述,当购买量小于5000千克时,选用甲方案付费少;在购买量等于5000千克时,两种方案相同;在购买量大于5000千克时,选用乙方案付费少.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在某地,人们发现某种蟋蟀1min,所叫次数x与当地温度T之间的关系或为T=ax+b,下面是蟋蟀所叫次数与温度变化情况对照表:
蟋蟀叫的次数(x)
…
84
98
119
…
温度(℃)T
…
15
17
20
…
①根据表中的数据确定a、b的值.
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题8分)某校为了解学生体质情况,从各年级学生中随机抽取部分学生进行体能测试.
每个学生的测试成绩按标准对应为优秀、良好、及格、不及格四个等级.统计员在将测试数据绘制 成图表时发现,优秀漏统计4人,良好漏统计6人,于是及时更正,从而形成如下图表.请按正确数据解答下列各题: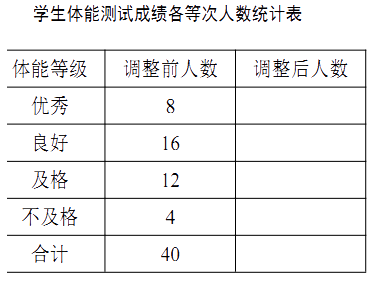
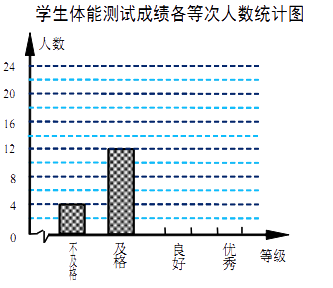
(1)填写统计表.
(2)根据调整后数据,补全条形统计图.
(3)若该校共有学生1500人,请你估算出该校体能测试等级为“优秀”的人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题6分)如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(2,2),B(4,1),C(4,4).

(1)作出 ABC关于原点O成中心对称的
ABC关于原点O成中心对称的  A1B1C1.
A1B1C1.
(2)作出点A关于x轴的对称点A'.若把点A'向右平移a个单位长度后落在 A1B1C1的内部(不包括顶点和边界),求a的取值范围.
A1B1C1的内部(不包括顶点和边界),求a的取值范围. -
科目: 来源: 题型:
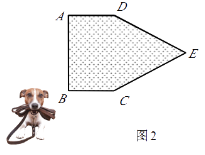
查看答案和解析>>【题目】在一空旷场地上设计一落地为矩形ABCD的小屋,AB+BC=10m.拴住小狗的10m长的绳子一端固定在B点处,小狗在不能进入小屋内的条件下活动,其可以活动的区域面积为S(m2).
①如图1,若BC=4m,则S=m.
②如图2,现考虑在(1)中的矩形ABCD小屋的右侧以CD为边拓展一正△CDE区域,使之变成落地为五边形ABCED的小屋,其它条件不变.则在BC的变化过程中,当S取得最小值时,边BC的长为m.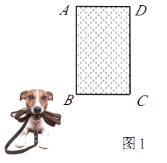
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(2,3)和点B(0,2),点A在反比例函数y=
 的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.
的图象上.作射线AB,再将射线AB绕点A按逆时针方向旋转45°,交反比例函数图象于点C,则点C的坐标为.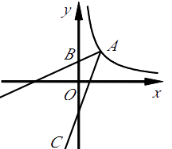
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了鼓励市民节约用水,自来水公司特制定了新的用水收费标准,每月用水量,x(吨)与应付水费(元)的函数关系如图.
(1)求出当月用水量不超过5吨时,y与x之间的函数关系式;
(2)某居民某月用水量为8吨,求应付的水费是多少?

相关试题

