搜索
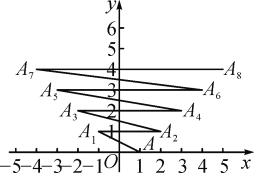
【题目】如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点A1(－1，1)，第二次点A1向右跳到A2(2，1)，第三次点A2跳到A3(－2，2)，第四次点A3向右跳动至点A4(3，2)，…，依此规律跳动下去，则点A2 019与点A2 020之间的距离是( )
A.2021B.2020C.2019D.2 018
参考答案：
【答案】A
【解析】
根据图形观察发现，第偶数次跳动至点的坐标，横坐标是次数的一半加上1，纵坐标是次数的一半，奇数次跳动与该偶数次跳动的横坐标的相反数加上1，纵坐标相同，可分别求出点
与点
的坐标，进而可求出点
与点
之间的距离．
解：观察发现，第2次跳动至点的坐标是
，
第4次跳动至点的坐标是
，
第6次跳动至点的坐标是
，
第8次跳动至点的坐标是
，
第
次跳动至点的坐标是
，
则第2020次跳动至点的坐标是
，
第2019次跳动至点的坐标是
．
点与点的纵坐标相等，
点与点之间的距离
，
故选：A．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图是二次函数y＝ax2＋bx＋c图象的一部分，图象过点A（－3，0），对称轴为直线x＝－1，给出四个结论：①b2＞4ac；②2a＋b＝0；③a＋b＋c＞0；④若点B（
，y1），C（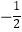 
，y2）为函数图象上的两点，则y1＜y2 ． 其中正确结论是 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】某移动通信公司推出了如下两种移动电话计费方式，
月使用费/元
主叫限定时间/分钟
主叫超时费（元/分钟）
方式一
30
600
0.20
方式二
50
600
0.25
说明：月使用费固定收取，主叫不超过限定时间不再收费，超过部分加收超时费．例如，方式一每月固定交费30元，当主叫计时不超过300分钟不再额外收费，超过300分钟时，超过部分每分钟加收0.20元（不足1分钟按1分钟计算）
（1）请根据题意完成如表的填空；
月主叫时间500分钟
月主叫时间800分钟
方式一收费/元
130
方式二收费/元
50
（2）设某月主叫时间为t（分钟），方式一、方式二两种计费方式的费用分别为y1（元），y2（元），分别写出两种计费方式中主叫时间t（分钟）与费用为y1（元），y2（元）的函数关系式；
（3）请计算说明选择哪种计费方式更省钱．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点E，F分别在边AD，CD上，
（1）若AB＝6，AE＝CF，点E为AD的中点，连接AE，BF．
①如图1，求证：BE＝BF＝3
；②如图2，连接AC，分别交AE，BF于M，M，连接DM，DN，求四边形BMDN的面积．
（2）如图3，过点D作DH⊥BE，垂足为H，连接CH，若∠DCH＝22.5°，则
的值为 （直接写出结果）． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，直线y＝2x+6交x轴于A，交y轴于B．
（1）直接写出A（ ， ），B（ ， ）；
（2）如图1，点E为直线y＝x+2上一点，点F为直线y＝
x上一点，若以A，B，E，F为顶点的四边形是平行四边形，求点E，F的坐标（3）如图2，点C（m，n）为线段AB上一动点，D（﹣7m，0）在x轴上，连接CD，点M为CD的中点，求点M的纵坐标y和横坐标x之间的函数关系式，并直接写出在点C移动过程中点M的运动路径长．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠A＝40°，点D在BC边上（不与C、D点重合），点P、点Q分别是AC、AB边上的动点，当△DPQ的周长最小时，则∠PDQ的度数为（ ）
A. 140°B. 120°C. 100°D. 70°
-
科目： 来源： 题型：
查看答案和解析>>【题目】完成下面的证明：
如图，AB和CD相交于点O，EF∥AB，∠C＝∠COA，∠D＝∠BOD．求证：∠A＝∠F．
证明：∵∠C＝∠COA，∠D＝∠BOD，
又∵∠COA＝∠BOD( )，
∴∠C＝ ( )．
∴AC∥BD( )．
∴∠A＝ ( )．
∵EF∥AB，
∴∠F＝ ( )．
∴∠A＝∠F( )．
相关试题
