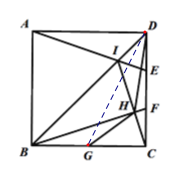
【题目】如图,E,F是正方形ABCD的边CD上两个动点,满足DE=CF.连接AE交BD于点I,连接BF交CI于点H,G为BC边上的中点.若正方形的边长为4,则线段DH长度的最小值是__________.

参考答案:
【答案】![]() -2
-2
【解析】
易证ADEBCF,得∠DAE=∠CBF,由A,C关于BD轴对称,得∠DAE=∠DCI,从而得∠CBF=∠DCI,进而得∠BHC=90°,结合G为BC边上的中点,得GH=2,连接DG,得DG=![]() ,根据三角形三边长关系,即可得到答案.
,根据三角形三边长关系,即可得到答案.
∵在正方形ABCD中,AD=BC,∠ADE=∠BCF=90°,
又∵DE=CF,
∴ADEBCF(ASA),
∴∠DAE=∠CBF,
∵A,C关于BD轴对称,
∴∠DAE=∠DCI,
∴∠CBF=∠DCI,
∴∠DCI+∠BCH=∠CBF+∠BCH=90°,
∴∠BHC=180°-(∠CBF+∠BCH)=180°-90°=90°,
∵G为BC边上的中点,
∴GH=![]() BC=2,
BC=2,
连接DG,则DG=![]() ,
,
∵在DHG中,DH>DG-GH,当且进当D,H,G三点共线时,DH=DG-GH=![]() -2,
-2,
∴线段DH长度的最小值是:![]() -2.
-2.
故答案是:![]() -2.
-2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB=18,BC=12,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则下列结论正确的个数是( )
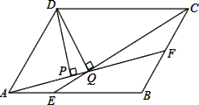
(1)CE平分∠BCD;(2)AF=CE;(3)连接DE、DF,则
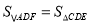 ;(4)DP:DQ=
;(4)DP:DQ=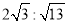
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
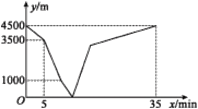
查看答案和解析>>【题目】小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行.小宁先出发5分钟后,小强骑自行车匀速回家.小宁开始跑步中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35分钟.两人之间的距离y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示.则当弟弟到家时,小宁离图书馆的距离为___________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=x+b与反比例函数y=
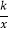 图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空)
图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数y1=
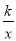 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图1的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图1,在四边形ABCD中,BC=AD,AB=

求证:四边形ABCD是 四边形.
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇同学的思路写出证明过程;
(3)用文字叙述所证命题的逆命题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,AB=2cm,BC=3cm,点P沿B→A→D运动,运动到点D时停止运动,点P运动的同时,另一点Q从B→C运动,速度是点P的一半,当点P停止运动时,点Q也停止运动.设点P运动的路程为xcm,其中设
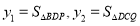 ,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.
,可可根据学习函数的经验,对函数y随自变量x的变化而变化的规律进行了探究,下面是可可的探究过程,请补充完整.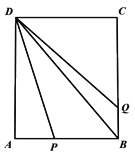
(1)如图是画出的函数
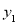 与x的函数图象,观察图象.当x=1时,
与x的函数图象,观察图象.当x=1时,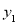 =_____;并写出函数的一条性质:________________________________________.
=_____;并写出函数的一条性质:________________________________________.(2)请帮助可可写出
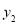 与x的函数关系式(不用写出取值范围)__________________.
与x的函数关系式(不用写出取值范围)__________________.(3)请按照列表、描点、连线的步骤在同一直角坐标系中,画出函数
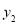 的图象.
的图象.(4)结合画出函数图象,解决问题:当
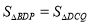 时,点P运动的路程x=_______.
时,点P运动的路程x=_______.
相关试题

