【题目】已知反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2).
(1)求这两个函数的关系式;
(2)观察图象,写出使得y1>y2成立的自变量x的取值范围;
(3)如果点C与点A关于x轴对称,求△ABC的面积.

参考答案:
【答案】(1) y1=![]() ,y2=2x+2;(2) x<-2或0<x<1;(3)12
,y2=2x+2;(2) x<-2或0<x<1;(3)12
【解析】试题分析:(1)把点A坐标代入反比例函数求出m的值,也就求出了反比例函数解析式,再把点B的坐标代入反比例函数解析式求出n的值,得到点B的坐标,然后利用待定系数法即可求出一次函数解析式;
(2)找出反比例函数在直线图形的上方的自变量x的取值即可;
(3)根据轴对称的性质求得C的坐标,过B点作BD⊥AC于D,求得AC、BD的长,根据三角形面积公式求得即可;
试题解析:
(1)∵点A(1,4)在反比例函数y1=![]() 的图象上,
的图象上,
∴k=1×4=4,
∴反比例函数的表达式为y1=![]() ,
,
∵点B(m,-2)也在反比例函数y1=![]() 的图象上,
的图象上,
∴-2=![]() ,解得m=-2,即B(-2,-2),
,解得m=-2,即B(-2,-2),
把点A(1,4),点B(-2,-2)代入一次函数y1=kx+b中,得
![]()
解得: ![]()
∴一次函数的表达式为y2=2x+2;
(2)∵y1>y2,
∴取反比例函数在直线图形的上方时自变量x的值即可,
由图形可得:当x<-2或0<x<1时,反比例函数在直线图形的上方,
∴当y1>y2成立的自变量x的取值范围x<-2或0<x<1;
(3)如图,过B点作BD⊥AC于D,如图所示:
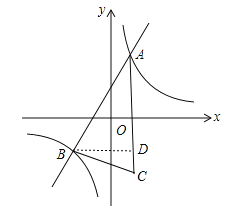
∵点C与点A关于x轴对称,
∴C(1,-4),
∴AC=8,BD=3,
∴S△ABC=![]() ACBD=12。
ACBD=12。
-
科目: 来源: 题型:
查看答案和解析>>【题目】工厂加工某种茶叶,计划一周生产
 千克,平均每天生产
千克,平均每天生产 千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负):
千克,由于各种原因实际每天产量与计划量相比有出入,某周七天的生产情况记录如下(超产为正、减产为负): ,
, ,
, ,
, ,
, ,
, ,
, .
.(
 )这一周的实际产量是多少千克?
)这一周的实际产量是多少千克?(
 )该厂规定工人工资参照平均产量计发,每千克
)该厂规定工人工资参照平均产量计发,每千克 元.若超产,则超产的部分每千克
元.若超产,则超产的部分每千克 元;若低于平均产量,按实际产量计发,而且每少
元;若低于平均产量,按实际产量计发,而且每少 千克扣除
千克扣除 元,那么该工厂工人这一周的工资总额是多少?
元,那么该工厂工人这一周的工资总额是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=
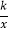 的一部分.请根据图中信息解答下列问题:
的一部分.请根据图中信息解答下列问题:(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D为BC边中点,P为AC边中点,E为BC上一点且BE=
 CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.
CE,连接AE,取AE中点Q并连接QD,取QD中点G,延长PG与BC边交于点H,若BC=6,则HE=_____.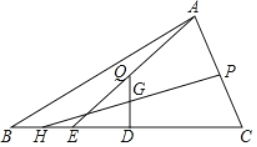
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数的图象经过点A(3,4)。
(1)这个函数的图象分布在哪些象限?y随x的增大如何变化?
(2)点B(2,6)、C( -2.5,-4.8 )和D(1,5)是否在这个函数的图象上?
-
科目: 来源: 题型:
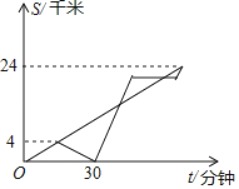
查看答案和解析>>【题目】在网红重庆,磁器口和洪崖洞是外地游客必到的打卡景点.现有一自行车队计划从磁器口到洪崖洞出发一段时间后,发现有贵重物品落在了磁器口,于是安排小南骑自行车以原速返回,剩下的成员速度不变向洪崖洞前进,小南取回物品后,改乘出租车追赶车队(取物品、等车时间忽略不计),小南在追赶上自行车队后仍乘坐出租车,再行驶10分钟后遭遇堵车,在此期间,自行车队反超出租车,拥堵30分钟后交通恢复正常,出租车以原速开往洪崖洞,最终出租车和自行车队同时到达,设自行车队和小南行驶时间为t(分钟),与磁器口距离s(千米),s与t的函数关系如图所示,则在第二次相遇后,出租车还经过了_____分钟到达洪崖洞.
-
科目: 来源: 题型:
查看答案和解析>>【题目】探究题.
如图,
 、
、 分别为数轴上的两点,
分别为数轴上的两点, 点对应的数为
点对应的数为 ,
, 点对应的数为
点对应的数为 .
.
(
 )请写出与
)请写出与 、
、 两点距离相等的点
两点距离相等的点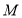 所对应的数.
所对应的数.(
 )现有一只电子蚂蚁
)现有一只电子蚂蚁 从
从 点出发,以
点出发,以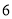 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁 恰好从
恰好从 点出发,以
点出发,以 单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的
单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的 点相遇,你知道
点相遇,你知道 点对应的数是多少吗?
点对应的数是多少吗?(
 )若当电子蚂蚁
)若当电子蚂蚁 从
从 点出发时,以
点出发时,以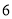 单位/秒的速度向左运动,同时另一只电子蚂蚁
单位/秒的速度向左运动,同时另一只电子蚂蚁 恰好从
恰好从 点出发,以
点出发,以 单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的
单位/秒的速度也向左运动,设两只电子蚂蚁在数轴上的 点相遇,你知道
点相遇,你知道 点对应的数是多少吗?
点对应的数是多少吗?
相关试题

