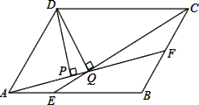
【题目】如图,平行四边形ABCD中,AB=18,BC=12,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则下列结论正确的个数是( )
(1)CE平分∠BCD;(2)AF=CE;(3)连接DE、DF,则![]() ;(4)DP:DQ=
;(4)DP:DQ=![]()
A.4个B.3个C.2个D.1个
参考答案:
【答案】B
【解析】
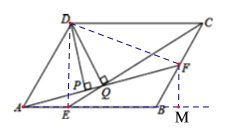
由平行四边形ABCD中,AB=18,BC=12,AE:EB=1:2,得EB= BC,结合AB∥CD,即可判断(1);过点F作FM⊥AB交AB的延长线于点M,在RtAMF中,利用勾股定理求出AF=![]() ,在BCE中,求出CE的值,即可判断(2);由
,在BCE中,求出CE的值,即可判断(2);由![]() ,
,![]() ,即可判断(3);由
,即可判断(3);由![]() ,即可判断(4).
,即可判断(4).
∵平行四边形ABCD中,AB=18,BC=12,AE:EB=1:2,
∴EB= BC=12,
∴∠BEC=∠BCE,
∵AB∥CD,
∴∠BEC=∠DCE,
∴∠BCE=∠DCE,
∴CE平分∠BCD,
∴(1)正确;
过点F作FM⊥AB交AB的延长线于点M,
∵AD∥BC,
∴∠CBM=∠DAB=60°,∠BFM=30°,
∵F是BC的中点,
∴BF=![]() BC=6,
BC=6,
∴BM=![]() BF=3,FM=
BF=3,FM=![]() BM=3
BM=3![]() ,
,
∴AM=18+3=21,
∴AF=![]() ,
,
∵EB= BC=12,∠ABC=180°-60°=120°,
∴CE=![]() ×BC=12
×BC=12![]() ,
,
∴AF≠CE,
∴(2)错误;
∵在平行四边形ABCD中,![]() ,
,![]() ,
,
∴![]() ,
,
∴(3)正确;
∵DP⊥AF,DQ⊥CE,![]()
∴![]() ,
,
∴DP:DQ=CE:AF=![]() ,
,
∴(4)正确.
故答案是:span>B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家,其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上,根据图中提供的信息,下列说法正确的是( )
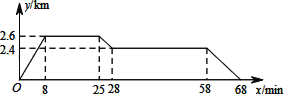
A.食堂离小明家2.4km
B.小明在图书馆呆了20min
C.小明从图书馆回家的平均速度是0.04km/min
D.图书馆在小明家和食堂之间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ACE是以平行四边行ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(10,-4
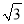 ),则D点的坐标是( )
),则D点的坐标是( )
A.(6,0)B.(6
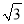 ,0)C.(8,0)D.(8
,0)C.(8,0)D.(8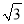 ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B在反比例函数y=
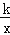 的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )
的图象上,过点A、B作x轴的垂线,垂足分别是M、N,射线AB交x轴于点C,若OM=MN=NC,四边形AMNB的面积是3,则k的值为( )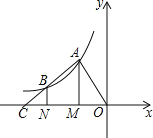
A.2 B.4 C.﹣2 D.﹣4
-
科目: 来源: 题型:
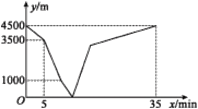
查看答案和解析>>【题目】小宁和弟弟小强分别从家和图书馆出发,沿同一条笔直的马路相向而行.小宁先出发5分钟后,小强骑自行车匀速回家.小宁开始跑步中途改为步行,且步行的速度为跑步速度的一半,到达图书馆恰好用了35分钟.两人之间的距离y(m)与小宁离开出发地的时间x(min)之间的函数图象如图所示.则当弟弟到家时,小宁离图书馆的距离为___________米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一次函数y=x+b与反比例函数y=
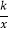 图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空)
图象,在第二象限内有两个交点,则k______0,b_______0,(用“>”、“<”、“=”填空) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F是正方形ABCD的边CD上两个动点,满足DE=CF.连接AE交BD于点I,连接BF交CI于点H,G为BC边上的中点.若正方形的边长为4,则线段DH长度的最小值是__________.

相关试题

