【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
∵∠1=∠2(已知),且∠1=∠4( )
∴∠2=∠4 (等量代换)
∴CE∥BF ( )
∴∠ =∠3( )
又∵∠B=∠C(已知),∴∠3=∠B(等量代换)
∴AB∥CD ( )

参考答案:
【答案】对顶角相等;同位角相等,两直线平行;C;两直线平行,同位角相等;内错角相等,两直线平行.
【解析】
第一个空根据对顶角的性质填写;第二、五个空根据平行线的判定填写;第三、四个空按平行线的性质填写.
∵∠1=∠2(已知),且∠1=∠4(对顶角相等),
∴∠2=∠4(等量代换),
∴CE∥BF(同位角相等,两直线平行),
∴∠C=∠3(两直线平行,同位角相等);
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换),
∴AB∥CD(内错角相等,两直线平行).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料I:
教材中我们学习了:若关于
 的一元二次方程
的一元二次方程 的两根为
的两根为
 ,根据这一性质,我们可以求出己知方程关于
,根据这一性质,我们可以求出己知方程关于 的代数式的值.
的代数式的值.问题解决:
(1)已知
 为方程
为方程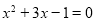 的两根,则:
的两根,则: __ _,
__ _, __ _,那么_
__ _,那么_ (请你完成以上的填空)
(请你完成以上的填空)阅读材料:II
已知
 ,且
,且 .求
.求 的值.
的值.解:由
 可知
可知


又
 且
且 ,即
,即
 是方程
是方程 的两根.
的两根.
问题解决:
(2)若
 且
且 则
则 ;
;(3)已知
 且
且 .求
.求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于两点
轴交于两点 和
和 与
与 轴交于点
轴交于点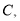 动点
动点 沿
沿 的边
的边 以每秒
以每秒 个单位长度的速度由起点
个单位长度的速度由起点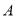 向终点
向终点 运动,过点
运动,过点 作
作 轴的垂线,交
轴的垂线,交 的另一边
的另一边 于点
于点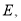 将
将 沿
沿 折叠,使点
折叠,使点 落在点
落在点 处,设点
处,设点 的运动时间为
的运动时间为 秒.
秒.
(1)求抛物线的解析式;
(2)N为抛物线上的点(点
 不与点
不与点 重合)且满足
重合)且满足 直接写出
直接写出 点的坐标;
点的坐标;(3)是否存在某一时刻
 ,使
,使 的面积最大,若存在,求出
的面积最大,若存在,求出 的值和最大面积;若不存在,请说明理由.
的值和最大面积;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】从甲地到乙地有
 三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:公交车用时的频数
公交车用时线路




合计

59
151
166
124
500

50
50
122
278
500

45
265
160
30
500
早高峰期间,乘坐_________(填“
 ”,“
”,“ ”或“
”或“ ”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图甲,直线y=﹣x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.

(1)求该抛物线的解析式;
(2)在该抛物线的对称轴上是否存在点M,使以C,P,M为顶点的三角形为等腰三角形?若存在,请直接写出所符合条件的点M的坐标;若不存在,请说明理由;
(3)当0<x<3时,在抛物线上求一点E,使△CBE的面积有最大值(图乙、丙供画图探究). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣1,1)、B(4,6)在抛物线y=ax2+bx上
(1)求抛物线的解析式;
(2)如图1,点F的坐标为(0,m)(m>2),直线AF交抛物线于另一点G,过点G作x轴的垂线,垂足为H.设抛物线与x轴的正半轴交于点E,连接FH、AE,求证:FH∥AE;
(3)如图2,直线AB分别交x轴、y轴于C、D两点.点P从点C出发,沿射线CD方向匀速运动,速度为每秒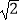
个单位长度;同时点Q从原点O出发,沿x轴正方向匀速运动,速度为每秒1个单位长度.点M是直线PQ与抛物线的一个交点,当运动到t秒时,QM=2PM,直接写出t的值.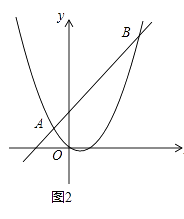
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC边长为10,P在AB上,Q在BC延长线,CQ=PA,过点P作PE⊥AC点E,过点P作PF∥BQ,交AC边于点F,连接PQ交AC于点D,则DE的长为_____.

相关试题

