【题目】已知一次函数 y=﹣2x﹣2
(1)根据关系式画出函数的图象.
(2)求出图象与 x 轴、y 轴的交点 A、B 的坐标.
(3)求 A、B 两点间的距离.
(4)y 的值随 x 值的增大怎样变化?

参考答案:
【答案】(1)A(﹣1,0),B(0,﹣2), 其图象如图所示见解析;(2)A(﹣1,0),B(0,﹣2);(3)A、B 两点间的距离为![]() ;(4)y 随 x 的增大而减小.
;(4)y 随 x 的增大而减小.
【解析】
(1)令x=0和y=0可先求得A、B的坐标,利用两点法可画出函数图象;
(2)由(1)可求得A、B的坐标;
(3)由A、B的坐标可求得OA、OB的长,利用勾股定理可求得AB的长;
(4)由一次函数的性质可求得其变化情况.
(1)在 y=﹣2x﹣2 中,令 y=0 可得 x=﹣1,令 x=0 可得 y=﹣2,
∴A(﹣1,0),B(0,﹣2),
其图象如图所示;

(2)由(1)可知 A(﹣1,0),B(0,﹣2);
(3)∵A(﹣1,0),B(0,﹣2),
∴OA=1,OB=2,
∴AB=![]() =
=![]() =
=![]() , 即 A、B 两点间的距离为
, 即 A、B 两点间的距离为![]() ;
;
(4)∵在 y=﹣2x﹣2 中,k=﹣2<0,
∴y 随 x 的增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,点A是x轴正半轴上的动点,点B坐标为(0,4),M是线段AB的中点,将点M绕点A顺时针方向旋转90°得到点C,过点C作x轴的垂线,垂足为F,过点B作y轴的垂线与直线CF相交于点E,点D是点A关于直线CF的对称点,连结AC,BC,CD,设点A的横坐标为t.

(1)当t=2时,求CF的长;
(2)①当t为何值时,点C落在线段BD上;
②设△BCE的面积为S,求S与t之间的函数关系式;
(3)如图2,当点C与点E重合时,将△CDF沿x轴左右平移得到△C′D′F′,再将A,B,C′,D′为顶点的四边形沿C′F′剪开,得到两个图形,用这两个图形拼成不重叠且无缝隙的图形恰好是三角形.请直接写出所有符合上述条件的点C′的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径为1,A、P、B、C是⊙O上的四个点,∠APC=∠CPB=60°.

(1)判断△ABC的形状:;
(2)试探究线段PA、PB、PC之间的数量关系,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)-102n×100×(-10)2n-1;
(2)[(-a)·(-b)2·a2b3c]2;
(3)(x3)2÷x2÷x-x3÷(-x)4·(-x4);
(4)(-9)3×
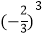 ×
× ;
;(5)xn+1·xn-1·x÷xm;
(6)a2·a3-(-a2)3-2a·(a2)3-2[(a3)3÷a3].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图。

(1)问题 如图1,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.求证: .
.
(2)探究 如图,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ时,上述结论是否依然成立?说明理由.
(3)应用 请利用(1)(2)获得的经验解决问题
如图3,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A.设点P的运动时间为t(秒),当以D为圆心,DC为半径的圆与AB相切时,求t的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某厂生产横截面直径为7cm的圆柱形罐头盒,需将“蘑菇罐头”字样贴在罐头侧面.为了获得较佳视觉效果,字样在罐头盒侧面所形成的弧的度数为90°,则“蘑菇罐头”字样的长度为( )

A. cm
cm
B. cm
cm
C. cm
cm
D.7πcm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 ABC中,
ABC中,  A=80
A=80 ,
,  ABC与
ABC与 ACD的平分线交于点A1,得
ACD的平分线交于点A1,得 A1;
A1;  A1BC与
A1BC与 A1CD的平分线相交于点A2,得
A1CD的平分线相交于点A2,得 A2;……;
A2;……;  A7BC与
A7BC与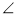 A7CD的平分线相交于点A8,得
A7CD的平分线相交于点A8,得 A8,则
A8,则 A8的度数为()
A8的度数为()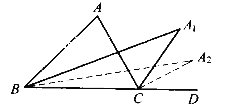
A.
 B.
B.  C.
C.  D.
D. 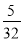
相关试题

