【题目】晓东在解一元二次方程时,发现有这样一种解法:如:解方程x(x+4)=6.
解:原方程可变形,得[(x+2)﹣2][(x+2)+2]=6.(x+2)2﹣22=6,(x+2)2=6+22,(x+2)2=10.直接开平方并整理,得![]() ,
,![]() .我们称晓东这种解法为“平均数法”.
.我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程(x+2)(x+6)=5时写的解题过程.
解:原方程可变形,得
[(x+□)﹣〇][(x+□)+〇]=5.
(x+□)2﹣〇2=5,
(x+□)2=5+〇2.
直接开平方并整理,得x1=☆,x2=¤.
上述过程中的“□”,“〇”,“☆”,“¤”表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣3)(x+1)=5.
参考答案:
【答案】(1)4,2,-1,-7;(2)
【解析】
(1)根据阅读材料中的信息,结合方程![]() 确定出上述过程中的“□”,“”,“☆”,“¤”表示的数即可;(2)利用“平均数法”解方程即可.
确定出上述过程中的“□”,“”,“☆”,“¤”表示的数即可;(2)利用“平均数法”解方程即可.
(1)4,2,-1,-7(最后两空可交换顺序);
故答案为:4,2,-1,-7;
(2)(x-3)(x+1)=5;
原方程可变形,得[(x-1)-2][(x-1)+2]=5,
整理得:(x-1)2-22=5,
(x-1)2=5+22,即(x-1)2=9,
直接开平方并整理,得x1=4,x2=-2.
-
科目: 来源: 题型:
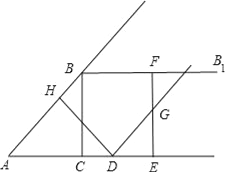
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,是摆放在张明和赵华面前的甲和乙两个圆柱形水槽从正面看到的图形,甲槽中有适量的水,乙槽中有一圆柱形铁块(圆柱形铁块的下底面完全落在水槽底面,铁块的高度低于水槽的高度).张明将甲槽中的水匀速注入乙槽,同时赵华计时并测量,最后他们把甲、乙两个水槽中水的深度
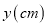 与注水时间
与注水时间 之间的关系画出了如图所示的函数图象.请根据函数图象提供的信息,解答下列问题:
之间的关系画出了如图所示的函数图象.请根据函数图象提供的信息,解答下列问题:(1)如图所示,线段
 表示 槽中水的深度与注水时间之间的关系;折线
表示 槽中水的深度与注水时间之间的关系;折线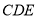 表示 槽中水的深度与注水时间之间的关系(以上两空填“甲” 或“乙”);点
表示 槽中水的深度与注水时间之间的关系(以上两空填“甲” 或“乙”);点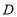 的纵坐标14表示的实际意义是 ;
的纵坐标14表示的实际意义是 ;(2)分别求线段
 、线段
、线段 的函数表达式;
的函数表达式;(3)注水多长时间时,甲、乙两个水槽中水的深度相同?
(4)若乙水槽的底面积为
 (水槽壁的厚度不计),求乙水槽中铁块的体积是多少
(水槽壁的厚度不计),求乙水槽中铁块的体积是多少 ?
?

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:

-
科目: 来源: 题型:
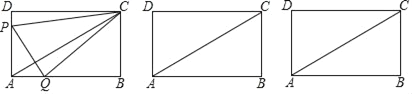
查看答案和解析>>【题目】如图①,在矩形ABCD中,AB=8,AD=4.点P从点A出发,沿A→D→C→D运动,速度为每秒2个单位长度;点Q从点A出发向点B运动,速度为每秒1个单位长度.P、Q两点同时出发,点Q运动到点B时,两点同时停止运动,设点Q的运动时间为t(秒).连结PQ、AC、CP、CQ.
(1)点P到点C时,t= ;当点Q到终点时,PC的长度为 ;
(2)用含t的代数式表示PD的长;
(3)当三角形CPQ的面积为9时,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有下列五个命题:①如果
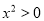 ,那么
,那么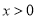 ;②内错角相等;③垂线段最短;④带根号的数都是无理数;⑤三角形的一个外角大于任何一个内角.其中真命题的个数为( )
;②内错角相等;③垂线段最短;④带根号的数都是无理数;⑤三角形的一个外角大于任何一个内角.其中真命题的个数为( )A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又 去早餐店吃早餐,然后散步走回家,其中 x 表示时间,y 表示张强离家的距离。根据图象提供的信息,以下四个说法错误的是( )

A. 体育场离张强家2.5千米 B. 张强在体育场锻炼了15分钟
C. 体育场离早餐店4千米 D. 张强从早餐店回家的平均速度是3千米/小时
相关试题

