【题目】下列条件中,不能判断△ABC是直角三角形的是( )
A. a:b:c=3:4:5 B. ∠A:∠B:∠C=3:4:5
C. ∠A+∠B=∠C D. a:b:c=1:2:![]()
参考答案:
【答案】B
【解析】
A、根据比值结合勾股定理的逆定理即可判断出三角形的形状;B、根据角的比值求出各角的度数,便可判断出三角形的形状;C、根据三角形的内角和为180度,即可计算出∠C的值;D、根据比值结合勾股定理的逆定理即可判断出三角形的形状.
A、因为a:b:c=3:4:5,所以设a=3x,b=4x,c=5x,则(3x)2+(4x)2=(5x)2,故为直角三角形,故A选项不符合题意;
B、因为∠A:∠B:∠C=3:4:5,所以设∠A=3x,则∠B=4x,∠C=5x,故3x+4x+5x=180°,解得x=15°,3x=15×3=45°,4x=15×4=60°,5x=15×5=75°,故此三角形是锐角三角形,故B选项符合题意;
C、因为∠A+∠B=∠C,∠A+∠B+∠C=180°,则∠C=90°,故为直角三角形,故C选项不符合题意;
D、因为a:b:c=1:2:![]() ,所以设a=x,b=2x,c=
,所以设a=x,b=2x,c=![]() x,则x2+(
x,则x2+(![]() x)2=(2x)2,故为直角三角形,故D选项不符合题意,
x)2=(2x)2,故为直角三角形,故D选项不符合题意,
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC=20cm,BC=16cm,D为AB中点,如果点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A运动,设运动时间为t(s).
(1)若点P与点Q的速度都是2cm/s,问经过多少时间△BPD与△CQP全等?说明理由;
(2)若点P的速度比点Q的速度都慢2cm/s,则经过多少时间△BPD与△CQP全等,并求出此时两点的速度;
(3)若点P、点Q分别以(2)中速度同时从B、C出发,都逆时针沿△ABC三边运动,问经过多少时间点P与点Q第一次相遇,相遇点在△ABC的哪条边上?并求出相遇点与点B的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )

A.0
B.2
C.4﹣2
D.2 ﹣2
﹣2 -
科目: 来源: 题型:
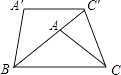
查看答案和解析>>【题目】如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程:①
 ;②
;② ;③
;③ ;④
;④ ;⑤
;⑤ ;⑥
;⑥ ,其中是二元一次方程的是( )
,其中是二元一次方程的是( )A.①B.①④C.①③D.①②④⑥
相关试题

