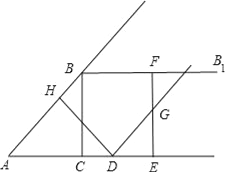
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
参考答案:
【答案】(1)当t=1时,AD=AB,AE=1;
(2)当t=![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 时,△DEG与△ACB相似.
时,△DEG与△ACB相似.
【解析】试题分析:(1)根据勾股定理得出AB=5,要使AD=AB=5,∵动点D每秒5个单位的速度运动,∴t=1;(2)当△DEG与△ACB相似时,要分两种情况讨论,根据相似三角形的性质,列出比例式,求出DE的表达式时,要分AD<AE和AD>AE两种情况讨论.
试题解析:
(1)∵∠ACB=90°,AC=3,BC=4, ∴AB=![]() =5.
=5.
∵AD=5t,CE=3t, ∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点, ∴GE=2.
当AD<AE(即t<![]() )时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 ![]() 或
或 ![]() ,
,
∴![]() 或
或![]() , ∴t=
, ∴t=![]() 或t=
或t=![]() ;
;
当AD>AE(即t>![]() )时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 ![]() 或
或 ![]() , ∴
, ∴![]() 或
或![]() ,
,
解得t=![]() 或t=
或t=![]() ;
;
综上所述,当t=![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 时,△DEG与△ACB相似.
时,△DEG与△ACB相似.
-
科目: 来源: 题型:
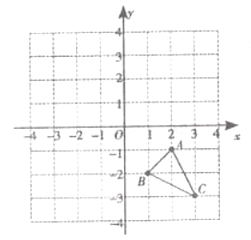
查看答案和解析>>【题目】如图:在平面直角坐标系中,已知
 的三个顶点的坐标分别为
的三个顶点的坐标分别为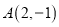 ,
,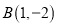 ,
,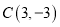 .
.
(1)将
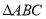 向上平移
向上平移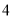 个单位长度,再向左平移
个单位长度,再向左平移 个单位长度,得到
个单位长度,得到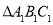 ,请画出
,请画出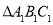 (点
(点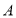 ,
,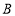 ,
,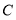 的对应点分别为
的对应点分别为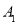 ,
,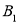 ,
,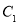 )
)(2)请画出与
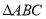 关于
关于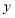 轴对称的
轴对称的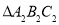 (点
(点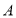 ,
,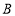 ,
,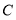 的对应点分别为
的对应点分别为 ,
,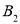 ,
,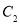 )
)(3)请写出
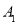 ,
, 的坐标
的坐标 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数y=mx+3的图象经过点A(2,6),B(n,-3).求:
(1)m,n的值;
(2)△OAB的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为20cm,∠ABC=120°.动点P、Q同时从点A出发,其中P以4cm/s的速度,沿A→B→C的路线向点C运动;Q以2
 cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.
cm/s的速度,沿A→C的路线向点C运动.当P、Q到达终点C时,整个运动随之结束,设运动时间为t秒.(1)在点P、Q运动过程中,请判断PQ与对角线AC的位置关系,并说明理由;
(2)若点Q关于菱形ABCD的对角线交点O的对称点为M,过点P且垂直于AB的直线l交菱形ABCD的边AD(或CD)于点N.
①当t为何值时,点P、M、N在一直线上?
②当点P、M、N不在一直线上时,是否存在这样的t,使得△PMN是以PN为一直角边的直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点E在△ABC内,∠ABC=∠EBD=α,∠ACB=∠EDB=60°,∠AEB=150°,∠BEC=90°.
(1)当α=60°时(如图1),
①判断△ABC的形状,并说明理由;
②求证:BD=
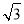 AE;
AE;(2)当α=90°时(如图2),求
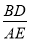 的值.
的值.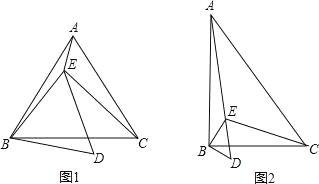
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC中,AD是∠BAC的角平分线,E为AD上一点,以BE为一边且在BE下方作等边△BEF,连接CF.
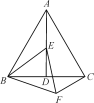
(1)求证:AE=CF;
(2)求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作:小明准备制作棱长为1cm的正方体纸盒,现选用一些废弃的圆形纸片进行如下设计:
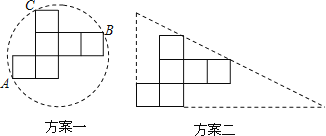
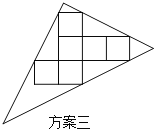
说明:方案一:图形中的圆过点A、B、C;
方案二:直角三角形的两直角边与展开图左下角的正方形边重合,斜边经过两个正方形的顶点.
纸片利用率=
 ×100%
×100%发现:(1)方案一中的点A、B恰好为该圆一直径的两个端点.
你认为小明的这个发现是否正确,请说明理由.
(2)小明通过计算,发现方案一中纸片的利用率仅约为38.2%.
请帮忙计算方案二的利用率,并写出求解过程.
探究:
(3)小明感觉上面两个方案的利用率均偏低,又进行了新的设计(方案三),请直接写出方案三的利用率.
相关试题

