【题目】如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
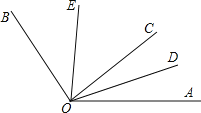
A. ∠DOE的度数不能确定 B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠AOD+∠BOE=60° D. ∠BOE=2∠COD
参考答案:
【答案】C
【解析】
A.∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠DOE=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=60°
∠AOB=60°
故本选项叙述错误;
B.∵OD是∠AOC的角平分线,
∴∠AOD=![]() ∠AOC.
∠AOC.
又∵OC是∠AOB内部任意一条射线,
∴∠AOC=∠EOC不一定成立。
故本选项叙述错误;
C.∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠BOE+∠AOD=∠EOC+∠DOC=∠DOE=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=60°
∠AOB=60°
故本选项叙述正确;
D.∵OC是∠AOB内部任意一条射线,
∴∠BOE=∠AOC不一定成立,
∴∠BOE=2∠COD不一定成立。
故本选项叙述错误;
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
已知:两条线段
 、
、 .
.
求作:菱形
 ,使得其对角线分别等于
,使得其对角线分别等于 和
和 .
.小军的作法如下:
如图

(
 )画一条线段
)画一条线段 等于
等于 .
.(
 )分别以
)分别以 、
、 为圆心,大于
为圆心,大于 的长为半径,在线段
的长为半径,在线段 的上下各作两条弧,两弧相交于
的上下各作两条弧,两弧相交于 、
、 两点.
两点.(
 )作直线
)作直线 交
交 于
于 点.
点.(
 )以
)以 点为圆心,线段
点为圆心,线段 的长为半径作两条弧,交直线
的长为半径作两条弧,交直线 于
于 、
、 两点,连接
两点,连接 、
、 、
、 、
、 .
.所以四边形
 就是所求的菱形.
就是所求的菱形.老师说:“小军的作法正确”.
该作图的依据是__________和___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列解题过程,然后回答问题:
解方程:

解:①当
 ≥0时,原方程可化为:
≥0时,原方程可化为:  ,解得
,解得 ;
;②当
 <0时,原方程可化为:
<0时,原方程可化为:  ,解得
,解得 ;
;所以原方程的解是
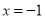 或
或
(1)解方程:

(2)探究:当
 为何值时,方程
为何值时,方程 ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。 -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).
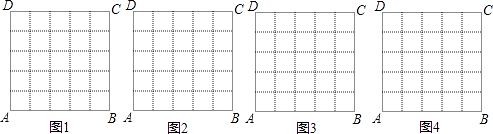
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在数轴上对应的数为2,若点B也在数轴上,且线段AB的长为4,C为AB的中点,则点C在数轴上对应的数为________.
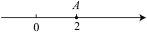
-
科目: 来源: 题型:
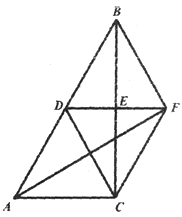
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF,AF.
(1)求证:四边形BDCF为菱形:
(2)若四边形BDCF的面积为24,CE:AC=2:3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
五个边长为
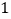 的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.
的小正方形如图①放置,要求用两条线段将它们分割成三部分后把它们拼接成一个新的正方形.


小辰是这样思考的:图①中五个边长为
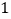 的小正方形的面积的和为
的小正方形的面积的和为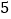 ,拼接后的正方形的面积也应该是
,拼接后的正方形的面积也应该是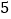 ,故而拼接后的正方形的边长为
,故而拼接后的正方形的边长为 ,因此想到了依据勾股定理,构造长为
,因此想到了依据勾股定理,构造长为 的线段,即:
的线段,即: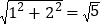 ,因此想到了两直角边分别为
,因此想到了两直角边分别为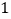 和
和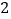 的直角三角形的斜边正好是
的直角三角形的斜边正好是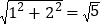 ,如图②,进而拼接成了一个便长为
,如图②,进而拼接成了一个便长为 的正方形.
的正方形. 参考上面的材料和小辰的思考方法,解决问题:
(
 )五个边长为
)五个边长为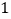 的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).
的小正方形如图④放置,类似图③,在图④中画出分割线和拼接后的正方形(只要画出一种即可).(
 )十个边长为
)十个边长为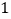 的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑤放置,类似图③,在图⑤中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).(
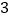 )五个边长为
)五个边长为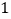 的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).
的小正方形如图⑥放置,类似图③,在图⑥中画出两条分割线将它们分割成三部分,并画出拼接后的正方形(只要画出一种即可).


相关试题

