【题目】先阅读下列解题过程,然后回答问题:
解方程: ![]()
解:①当![]() ≥0时,原方程可化为:
≥0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
②当![]() <0时,原方程可化为:
<0时,原方程可化为: ![]() ,解得
,解得![]() ;
;
所以原方程的解是![]() 或
或![]()
(1)解方程: ![]()
(2)探究:当![]() 为何值时,方程
为何值时,方程![]() ①无解;②只有一个解;③有两个解。
①无解;②只有一个解;③有两个解。
参考答案:
【答案】(1)![]() 或
或![]() (2)
(2)![]() <
<![]() 时,方程
时,方程![]() 无解;
无解; ![]() =
=![]() 时,方程只有一个解;即
时,方程只有一个解;即![]() >
>![]() 时,方程
时,方程![]() 有两个解
有两个解
【解析】试题分析:(1)首先要认真审题,解此题时要理解绝对值的意义,要会去绝对值,然后化为一元一次方程即可求得.
(2)运用分类讨论进行解答.
试题解析:(1)当3x-2≥0时,原方程可化为:3x-2=4,
解得x=2;
当3x-2<0时,原方程可化为:3x-2=-4,
解得x=-![]() .
.
所以原方程的解是x=2或x=-![]() ;
;
(2)∵|x-2|≥0,
∴当b+1<0,即b<-1时,方程无解;
当b+1=0,即b=-1时,方程只有一个解;
当b+1>0,即b>-1时,方程有两个解.
-
科目: 来源: 题型:
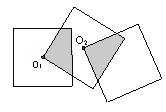
查看答案和解析>>【题目】如图,三个边长均为2的正方形重叠在一起,O1、O2是其中两个正方形的中心,则阴影部分的面积是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某城市市民广场一入口处有五级高度相等的小台阶.已知台阶总高1.5米,为了安全,现要做一个不锈钢扶手AB及两根与FG垂直且长为1米的不锈钢架杆AD和BC(杆子的底端分别为D、C),且∠DAB=66.5°.(参考数据:cos66.5°≈0.40,sin66.5°≈0.92)
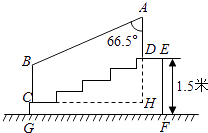
(1)求点D与点C的高度差DH;
(2)求所有不锈钢材料的总长度(即AD+AB+BC的长,结果精确到0.1米) -
科目: 来源: 题型:
查看答案和解析>>【题目】在数学课上,老师提出如下问题:
尺规作图:作对角线等于已知线段的菱形.
已知:两条线段
 、
、 .
.
求作:菱形
 ,使得其对角线分别等于
,使得其对角线分别等于 和
和 .
.小军的作法如下:
如图

(
 )画一条线段
)画一条线段 等于
等于 .
.(
 )分别以
)分别以 、
、 为圆心,大于
为圆心,大于 的长为半径,在线段
的长为半径,在线段 的上下各作两条弧,两弧相交于
的上下各作两条弧,两弧相交于 、
、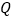 两点.
两点.(
 )作直线
)作直线 交
交 于
于 点.
点.(
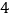 )以
)以 点为圆心,线段
点为圆心,线段 的长为半径作两条弧,交直线
的长为半径作两条弧,交直线 于
于 、
、 两点,连接
两点,连接 、
、 、
、 、
、 .
.所以四边形
 就是所求的菱形.
就是所求的菱形.老师说:“小军的作法正确”.
该作图的依据是__________和___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,老师要求学生在5×5的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行.画四种图形,并直接写出其周长(所画图象相似的只算一种).
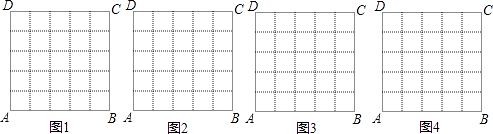
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
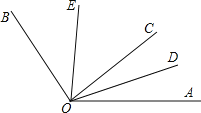
A. ∠DOE的度数不能确定 B. ∠AOD=
 ∠EOC
∠EOCC. ∠AOD+∠BOE=60° D. ∠BOE=2∠COD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在数轴上对应的数为2,若点B也在数轴上,且线段AB的长为4,C为AB的中点,则点C在数轴上对应的数为________.
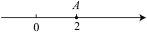
相关试题

