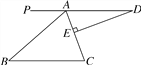
【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
参考答案:
【答案】(1)△ABC是等腰三角形,∠B=40°;(2)见解析.
【解析】(1)、根据Rt△ADE的内角和得出∠DAC=70°,根据平行线的性质得出∠C=70°,从而根据有两个角相等的三角形是等腰三角形得出答案;(2)、根据等腰三角形底边上的三线合一定理得出DB为顶角的角平分线.
解:(1)∵DE⊥AC于点E,∠D=20°,∴∠CAD=70°, ∵AD∥BC,
∴∠C=∠CAD=70°, 又∵∠BAC=70°,∴∠BAC=∠C,∴AB=BC,
∴△ABC是等腰三角形,∴∠B=180°-∠BAC-∠C=180°-70°-70°=40°.
(2)∵延长线段DE恰好过点B,DE⊥AC,∴BD⊥AC,∵△ABC是等腰三角形,
∴DB是∠ABC的平分线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣2(m+1)x+m(m+2)
(1)求证:无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值.
(2)若该函数图象的对称轴为直线x=2,试求二次函数的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对x,y定义一种新运算x[]y=
 (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2= 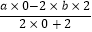 =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
(2)若x[]y=y[]x,对任意实数x,y都成立(这里x[]y和y[]x均有意义),求a与b的函数关系式? -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
⑴

(2)

(3)
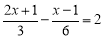 .
.(4)

(5)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形一腰上的中线将三角形的周长分为9cm和15cm两部分,求这个等腰三角形的底边长和腰长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)3x=-9x-12
(2)

(3)
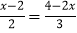
(4)

相关试题

