【题目】已知二次函数y=x2﹣2(m+1)x+m(m+2)
(1)求证:无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值.
(2)若该函数图象的对称轴为直线x=2,试求二次函数的最小值.
参考答案:
【答案】
(1)证明:设抛物线与x轴的两交点分别为(a,0),(b,0),
则a+b=2(m+1),ab=m(m+2),
所以|a﹣b|= ![]() =
= ![]() =
= ![]() =2,
=2,
即无论m为任何实数,该函数图象与x轴两个交点之间的距离为定值
(2)解:根据题意得x=﹣ ![]() =2,解得m=0,
=2,解得m=0,
则抛物线解析式为y=x2﹣2x=(x﹣1)2﹣1,
所以二次函数的最小值为﹣1
【解析】(1)设抛物线与x轴的两交点分别为(a,0),(b,0),根据抛物线与x轴的交点问题,得到方程x2﹣2(m+1)x+m(m+2)=0的两根分别为a与b,根据根与系数的关系得a+b=2(m+1),ab=m(m+2),而函数图象与x轴两个交点之间的距离可表示为|a﹣b|,然后根据代数式的变形得到|a﹣b|= ![]() =
= ![]() ,再利用整体代入的方法得到|a﹣b|=
,再利用整体代入的方法得到|a﹣b|= ![]() =2,由此可判断函数图象与x轴两个交点之间的距离为定值.(2)根据抛物线的对称轴方程得到x=﹣
=2,由此可判断函数图象与x轴两个交点之间的距离为定值.(2)根据抛物线的对称轴方程得到x=﹣ ![]() =2,解得m=0,则抛物线解析式为y=x2﹣2x,然后配成顶点式得到二次函数的最小值.
=2,解得m=0,则抛物线解析式为y=x2﹣2x,然后配成顶点式得到二次函数的最小值.
【考点精析】本题主要考查了二次函数的最值和抛物线与坐标轴的交点的相关知识点,需要掌握如果自变量的取值范围是全体实数,那么函数在顶点处取得最大值(或最小值),即当x=-b/2a时,y最值=(4ac-b2)/4a;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能正确解答此题.
-
科目: 来源: 题型:
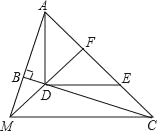
查看答案和解析>>【题目】如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD、AB的延长线相交于点M,连接MC.
(1)求证:∠FMC=∠FCM;
(2)将条件中的AD⊥DE与(1)中的结论互换,其他条件不变,命题是否正确?请给出理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的直角坐标系中,解答下列问题:
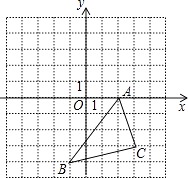
(1)分别写出A、B两点的坐标;
(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;
(3)求出线段B1A所在直线l的函数解析式,并写出在直线l上从B1到A的自变量x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,∠ABC=2∠C,BE平分∠ABC交AC于E,AD⊥BE于D,下列结论:①AC﹣BE=AE;②点E在线段BC的垂直平分线上;③∠DAE=∠C;④BC=4AD,其中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对x,y定义一种新运算x[]y=
 (其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2=
(其中a,b均为非零常数),这里等式右边是通常的四则混合运算,例如:0[]2= 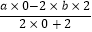 =﹣2b.
=﹣2b.
(1)已知1[]2=3,﹣1[]3=﹣2.请解答下列问题.
①求a,b的值;
②若M=(m2﹣m﹣1)[](2m﹣2m2),则称M是m的函数,当自变量m在﹣1≤m≤3的范围内取值时,函数值M为整数的个数记为k,求k的值;
(2)若x[]y=y[]x,对任意实数x,y都成立(这里x[]y和y[]x均有意义),求a与b的函数关系式? -
科目: 来源: 题型:
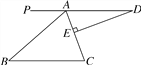
查看答案和解析>>【题目】如图,AD∥BC,∠BAC=70°,DE⊥AC于点E,∠D=20°.
(1)求∠B的度数,并判断△ABC的形状;
(2)若延长线段DE恰好过点B,试说明DB是∠ABC的平分线.
相关试题

