【题目】【现场学习】
定义:我们把绝对值符号内含有未知数的方程叫做“含有绝对值的方程”.
如:|x|=2,|2x﹣1|=3,| ![]() |﹣x=1,…都是含有绝对值的方程.
|﹣x=1,…都是含有绝对值的方程.
怎样求含有绝对值的方程的解呢?基本思路是:含有绝对值的方程→不含有绝对值的方程.
我们知道,根据绝对值的意义,由|x|=2,可得x=2或x=﹣2.
(1)[例]解方程:|2x﹣1|=3.
我们只要把2x﹣1看成一个整体就可以根据绝对值的意义进一步解决问题.
解:根据绝对值的意义,得2x﹣1=3或2x﹣1= .
解这两个一元一次方程,得x=2或x=﹣1.
检验:
①当x=2时,
原方程的左边=|2x﹣1|=|2×2﹣1|=3,
原方程的右边=3,
∵左边=右边
∴x=2是原方程的解.
②当x=﹣1时,
原方程的左边=|2x﹣1|=|2×(﹣1)﹣1|=3,
原方程的右边=3,
∵左边=右边
∴x=﹣1是原方程的解.
综合①②可知,原方程的解是:x=2,x=﹣1.
【解决问题】
解方程:| ![]() |﹣x=1.
|﹣x=1.
(2)【解决问题】解方程:| ![]() |﹣x=1.
|﹣x=1.
参考答案:
【答案】
(1)-3
(2)【解答】解:原方程变形为:| x 1 2 |=x+1,
根据绝对值的意义,得 ![]() =1+x或
=1+x或 ![]() =﹣(1+x),
=﹣(1+x),
解得:x=﹣3或 x=﹣ ![]() ,
,
经检验:x=﹣3不是原方程的解,x=﹣ ![]() 是原方程的解,
是原方程的解,
所以,原方程的解是:x=﹣ ![]() .
.
【解析】根据解方程的步骤去分母、去括号、移项、合并同类项、系数化为一;由绝对值的意义,得到两个方程,分别求出x的值,经检验得到原方程的解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=90°,AB=AC=3,点D在BC上且BD=2CD,E,F分别在AB,AC上运动且始终保持∠EDF=45°,设BE=x,CF=y,则y与x之间的函数关系用图象表示为:( )

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下面的频数分布表:
次数
60≤x<90
90≤x<120
120≤x<150
150≤x<180
180≤x<210
频数
16
25
9
7
3
(1)全班有多少同学?
(2)组距是多少?组数是多少?
(3)跳绳次数x在120≤x<180范围的同学有多少?占全班同学的百分之几?
(4)画出适当的统计图表示上面的信息. -
科目: 来源: 题型:
查看答案和解析>>【题目】如不等式组
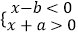 解集为2<x<3,则a,b的值分别为( )
解集为2<x<3,则a,b的值分别为( )
A.﹣2,3
B.2,﹣3
C.3,﹣2
D.﹣3,2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的周长是 (3x22) cm,第一条边长度是( 5xx2 )cm,第二条边比第一条边长 (3x210x+6) cm,则第三条边的长度是( )cm.
A. 2x28
2x28
B. x2+6
x2+6
C.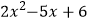
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC⊥BC,CD⊥AB,DE⊥BC,垂足分别为C,D,E,则下列说法不正确的是( )
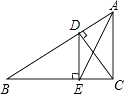
A.AC是△ABC的高
B.DE是△BCD的高
C.DE是△ABE的高
D.AD是△ACD的高
相关试题

