搜索
【题目】一只不透明的箱子里共有3个球，把它们的分别编号为1，2，3，这些球除编号不同外其余都相同．
（1）从箱子中随机摸出一个球，求摸出的球是编号为1的球的概率；
（2）从箱子中随机摸出一个球，记录下编号后将它放回箱子，搅匀后再摸出一个球并记录下编号，求两次摸出的球都是编号为3的球的概率．
参考答案：
【答案】
（1）解：从箱子中随机摸出一个球，摸出的球是编号为1的球的概率为： 
；
（2）解：画树状图如下：
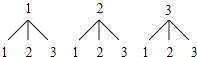
共有9种等可能的结果，两次摸出的球都是编号为3的球的概率为 
．
【解析】（1）直接利用概率公式求解即可；（2）首先列出树状图，然后利用概率公式求解即可．
【考点精析】本题主要考查了列表法与树状图法和概率公式的相关知识点，需要掌握当一次试验要设计三个或更多的因素时，用列表法就不方便了，为了不重不漏地列出所有可能的结果，通常采用树状图法求概率；一般地，如果在一次试验中，有n种可能的结果，并且它们发生的可能性都相等，事件A包含其中的m中结果，那么事件A发生的概率为P（A）=m/n才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为迎接“六一”儿童节的到来，某校学生参加献爱心捐款活动，随机抽取该校部分学生的捐款数进行统计分析，相应数据的统计图如下：
（1）该样本的容量是 ， 样本中捐款15元的学生有人；
（2）若该校一共有500名学生，据此样本估计该校学生的捐款总数． -
科目： 来源： 题型：
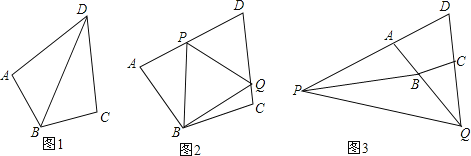
查看答案和解析>>【题目】已知在四边形ABCD中，∠ABC+∠ADC=180°，AB=BC．
（1）如图1，若∠BAD=90°，AD=2，求CD的长度；
（2）如图2，点P、Q分别在线段AD、DC上，满足PQ=AP+CQ，求证：∠PBQ=90°
∠ADC；（3）如图3，若点Q运动到DC的延长线上，点P也运动到DA的延长线上时，仍然满足PQ=AP+CQ，则（2）中的结论是否成立？若成立，请给出证明过程，若不成立，请写出∠PBQ与∠ADC的数量关系，并给出证明过程.
-
科目： 来源： 题型：
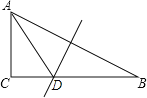
查看答案和解析>>【题目】如图，Rt△ABC中，∠C=90°，BC=15，斜边AB的垂直平分线与∠CAB的平分线都交BC于D点，则点D到斜边AB的距离为___________.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系xOy中，如图，已知Rt△DOE，∠DOE=90°，OD=3，点D在y轴上，点E在x轴上，在△ABC中，点A，C在x轴上，AC=5．∠ACB+∠ODE=180°，∠ABC=∠OED，BC=DE．按下列要求画图（保留作图痕迹）：
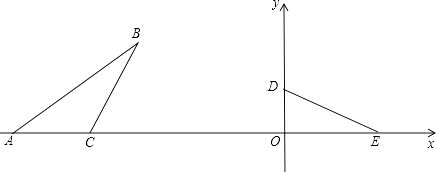
（1）将△ODE绕O点按逆时针方向旋转90°得到△OMN（其中点D的对应点为点M，点E的对应点为点N），画出△OMN；
（2）将△ABC沿x轴向右平移得到△A′B′C′（其中点A，B，C的对应点分别为点A′，B′，C′），使得B′C′与（1）中的△OMN的边NM重合；
（3）求OE的长． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：△ABC中，AB=AC，∠BAC=90°．
（1）如图（1），CD平分∠ACB交AB于点D，BE⊥CD于点E，延长BE、CA相交于点F，请猜想线段BE与CD的数量关系，并说明理由．
（2）如图（2），点F在BC上，∠BFE=
∠ACB，BE⊥FE于点E，AB与FE交于点D，FH∥AC交AB于H，延长FH、BE相交于点G，求证：BE=FD；（3）如图（3），点F在BC延长线上，∠BFE=
∠ACB，BE⊥FE于点E，FE交BA延长线于点D，请你直接写出线段BE与FD的数量关系（不需要证明）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某小商场以每件20元的价格购进一种服装，先试销一周，试销期间每天的销量（件）与每件的销售价x（元/件）如下表：
x（元/件）
38
36
34
32
30
28
26
t（件）
4
8
12
16
20
24
28
假定试销中每天的销售量t（件）与销售价x（元/件）之间满足一次函数．
（1）试求t与x之间的函数关系式；
（2）在商品不积压且不考虑其它因素的条件下，每件服装的销售定价为多少时，该小商场销售这种服装每天获得的毛利润最大？每天的最大毛利润是多少？（注：每件服装销售的毛利润=每件服装的销售价﹣每件服装的进货价）
相关试题
