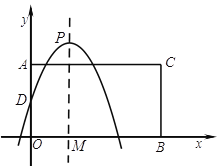
【题目】如图, 在平面直角坐标系中,点A,B分别是![]() 轴正半轴,
轴正半轴, ![]() 轴正半轴上两动点,
轴正半轴上两动点, ![]() ,
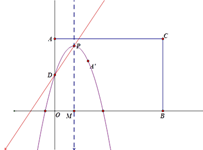
, ![]() ,以AO,BO为邻边构造矩形AOBC,抛物线
,以AO,BO为邻边构造矩形AOBC,抛物线![]() 交
交![]() 轴于点D,P为顶点,PM⊥
轴于点D,P为顶点,PM⊥![]() 轴于点M.
轴于点M.
(1)求![]() ,
, ![]() 的长(结果均用含
的长(结果均用含![]() 的代数式表示).
的代数式表示).
(2)当![]() 时,求该抛物线的表达式.
时,求该抛物线的表达式.
(3)在点![]() 在整个运动过程中.
在整个运动过程中.
①若存在![]() 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的![]() 的值.
的值.
②当点A关于直线DP的对称点![]() 恰好落在抛物线
恰好落在抛物线![]() 的图象上时,请直接写出
的图象上时,请直接写出![]() 的值.
的值.
参考答案:
【答案】(1)OD长为k,PM的长为k+3;
(2)该抛物线的表达式为![]() ;
;
(3)①满足条件的![]() 的值为
的值为![]() , 6,或
, 6,或![]()
②![]() 的值为
的值为![]() .
.
【解析】(1)点D在y=﹣x2+3x+k上,且在y轴上,即y=0求出点D坐标,根据抛物线顶点公式,求出即可;
(2)先用k表示出相关的点的坐标,根据PM=BM建立方程即可;
(3)①先用k表示出相关的点的坐标,根据△ADP是等腰三角形,分三种情况,AD=AP,DA=DP,PA=PD计算;
②由点P,D坐标求出直线PD解析式,根据PD⊥AA′,且A(0,2k),确定出AA′解析式,继而求出交点,再求出A′的坐标即可.
解:(1)把x=0,代入![]() ,得
,得![]() .∴
.∴![]() .
.
∵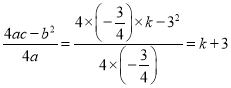 ,∴
,∴![]() .
.
(2)∵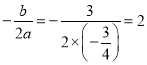 ,∴
,∴![]() ,
, ![]() .
.
又∵![]() ,
, ![]() ,∴
,∴![]() ,解得
,解得![]() .
.
∴该抛物线的表达式为![]() .
.
(3)①
Ⅰ)当点P在矩形AOBC外部时
如图所示,
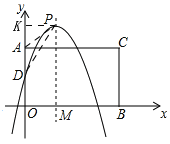
过P作PK⊥OA于点K,当AD=AP时,
∵AD=AO-DO=2k-k=k,
∴AD=AP =k,KA=KO-AO=PM-AO= ![]()
KP=OM=2,在Rt△KAP中, ![]()
∴![]() ,解得
,解得![]() .
.
Ⅱ)当点P在矩形AOBC内部时
当PD=AP时,如图所示,

过P作PH⊥OA于H,
AD=k,HD=![]() ,
, ![]()
又∵HO=PM= ![]() ,
,
∴![]() ,解得
,解得![]() .
.
当DP=DA时,如图所示,

过D作PQ⊥PM于Q,
PQ=PM-QM=PM-OD= ![]()
DQ=OM=2,DP=DA=k,
在Rt△DQP中, ![]() .
.
∴![]() .
.
②![]() .
.
“点睛”此题是二次函数综合题,主要考查了二次函数解析式的确定,平面坐标系中求线段的长,等腰三角形的性质,确定出函数解析式是解本题的关键. 解(3)是本题的难点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若△ABC∽△A′B′C′,相似比为1∶2,则△ABC与△A′B′C′的面积的比为( )
A.1∶2B.2∶1C.1∶4D.4∶1
-
科目: 来源: 题型:
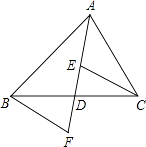
查看答案和解析>>【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为( )
A.20%
B.40%
C.﹣220%
D.30% -
科目: 来源: 题型:
查看答案和解析>>【题目】已知x,y都是自然数,且有x(x﹣y)﹣y(y﹣x)=12,求x、y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据所学知识填空.
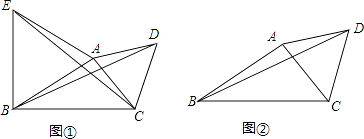
(1)如图①,△ABE,△ACD都是等边三角形,若CE=6,则BD的长=;
(2)如图②,△ABC中,∠ABC=30°,AB=3,BC=4,D是△ABC外一点,且△ACD是等边三角形,则BD的长= . -
科目: 来源: 题型:
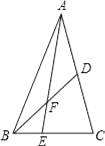
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF= .
相关试题

