【题目】如图,AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF、CE,且∠FBD=35°,∠BDF=75°,下列说法:①△BDF≌CDE;②ABD和△ACD面积相等;③BF∥CE;④∠DEC=70°,其中正确的有( ) 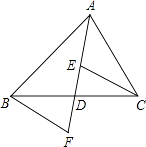
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】D
【解析】解:∵AD是△ABC的中线, ∴BD=CD,
∴△ABD的面积=△ACD的面积,
在△BDF和△CDE中, 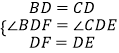 ,
,
∴△BDF≌△CDE(SAS),故①②正确
∴∠F=∠CED,∠DEC=∠F,
∴BF∥CE,故③正确,
∵∠FBD=35°,∠BDF=75°,
∴∠F=180°﹣35°﹣75°=70°,
∴∠DEC=70°,故④正确;
综上所述,正确的是①②③④4个.
故答案为:D.
根据三角形中线的定义可得BD=CD,得出△ABD的面积=△ACD的面积,然后利用“边角边”证明△BDF和△CDE全等,由全等三角形的性质得出∠F=∠CED,∠DEC=∠F,再根据内错角相等,两直线平行可得BF∥CE,最后根据三角形内角和定理求出∠F,得出④正确,即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,作AD⊥AB交BC的延长线于点D,作CE⊥AC,且使AE∥BD,连结DE.
(1)求证:AD=CE.
(2)若DE=3,CE=4,求tan∠DAE的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,弦AB=弦CD,AB⊥CD于点E,且AE<EB,CE<ED,连结AO,DO,BD.
(1)求证:EB=ED.
(2)若AO=6,求
 的长.
的长.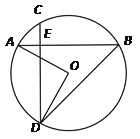
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明尝试着将矩形纸片ABCD(如图①,AD>CD)沿过A点的直线折叠,使得B点落在AD边上的点F处,折痕为AE(如图②);再沿过D点的直线折叠,使得C点落在DA边上的点N处,E点落在AE边上的点M处,折痕为DG(如图③).如果第二次折叠后,M点正好在∠NDG的平分线上,那么矩形ABCD的长BC与宽AB的关系是( )
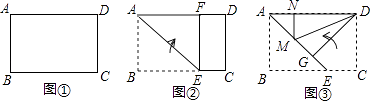
A.BC=2AB
B.BC=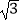 AB
AB
C.BC=1.5AB
D.BC=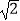 AB
AB -
科目: 来源: 题型:
查看答案和解析>>【题目】已知 x=﹣1 是一元二次方程 ax2﹣bx+6=0 的一个根,则 a+b 的值为_____
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP,CP的延长线分别交AD于点E,F,连结BD,DP,BD与CF相交于点H.给出下列结论: ①△ABE≌△DCF;②△DPH是等腰三角形;③PF=
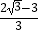 AB;④
AB;④  =
= 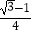 .
.
其中正确结论的个数是( )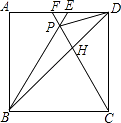
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】某校准备去楠溪江某景点春游,旅行社面向学生推出的收费标准如下:
人数m
0<m≤100
100<m≤200
m>200
收费标准(元/人)
90
80
70
已知该校七年级参加春游学生人数多于100人,八年级参加春游学生人数少于100人.经核算,若两个年级分别组团共需花费17700元,若两个年级联合组团只需花费14700元.
(1)两个年级参加春游学生人数之和超过200人吗?为什么?
(2)两个年级参加春游学生各有多少人?
相关试题

