【题目】根据所学知识填空. 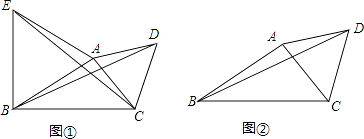
(1)如图①,△ABE,△ACD都是等边三角形,若CE=6,则BD的长=;
(2)如图②,△ABC中,∠ABC=30°,AB=3,BC=4,D是△ABC外一点,且△ACD是等边三角形,则BD的长= .
参考答案:
【答案】
(1)6
(2)5
【解析】(1)解:∵△ABE和△ACD是等边三角形, ∴BE=AE=AB=3,AD=AC,∠ABE=∠EAB=∠DAC=60°,
∴∠EAB+∠BAC=∠DAC+∠CAB,
∴∠BAD=∠EAC,
在△ACE和△ADB中,  ,
,
∴△ACE≌△ADB(SAS),
∴BD=CE=6;
所以答案是:6;
(2.)作等边三角形ABE,连接AE,如图所示:
则AE=AB=3,∠ABE=60°,
∵∠ABC=30°,
∴∠CBE=∠ABE+∠ABC=90°,
∴CE= ![]() =
= ![]() =5,
=5,
由(1)得:BD=CE=5;
所以答案是:5.
【考点精析】本题主要考查了等边三角形的性质的相关知识点,需要掌握等边三角形的三个角都相等并且每个角都是60°才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县大力推进义务教育均衡发展,加强学校标准化建设,计划用三年时间对全县学校的设施和设备进行全面改造,2014年县政府已投资5亿元人民币,若每年投资的增长率相同,预计2016年投资7.2亿元人民币,那么每年投资的增长率为( )
A.20%
B.40%
C.﹣220%
D.30% -
科目: 来源: 题型:
查看答案和解析>>【题目】如图, 在平面直角坐标系中,点A,B分别是
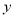 轴正半轴,
轴正半轴, 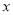 轴正半轴上两动点,
轴正半轴上两动点, 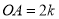 ,
,  ,以AO,BO为邻边构造矩形AOBC,抛物线
,以AO,BO为邻边构造矩形AOBC,抛物线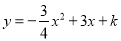 交
交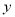 轴于点D,P为顶点,PM⊥
轴于点D,P为顶点,PM⊥ 轴于点M.
轴于点M.(1)求
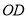 ,
, 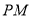 的长(结果均用含
的长(结果均用含 的代数式表示).
的代数式表示).(2)当
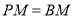 时,求该抛物线的表达式.
时,求该抛物线的表达式.(3)在点
 在整个运动过程中.
在整个运动过程中.①若存在
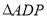 是等腰三角形,请求出所有满足条件的
是等腰三角形,请求出所有满足条件的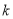 的值.
的值.②当点A关于直线DP的对称点
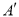 恰好落在抛物线
恰好落在抛物线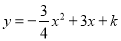 的图象上时,请直接写出
的图象上时,请直接写出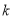 的值.
的值.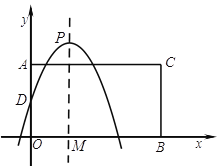
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x,y都是自然数,且有x(x﹣y)﹣y(y﹣x)=12,求x、y的值.
-
科目: 来源: 题型:
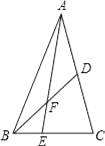
查看答案和解析>>【题目】如图,在△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,设△ABC,△ADF,△BEF的面积分别为S△ABC , S△ADF , S△BEF , 且S△ABC=12,则S△ADF﹣S△BEF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】多项式3x|m|y2+(m+2)x2y﹣1是四次三项式,则m的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】实验室里,水平桌面上有甲、乙两个圆柱形容器(容器足够高),底面半径之比为1∶2,用一个管子在甲、乙两个容器的15厘米高度处连通(即管子底端离容器底15厘米).已知只有乙容器中有水,水位高2厘米,如图所示.现同时向甲、乙两个容器注水,平均每分钟注入乙容器的水量是注入甲容器水量的k倍.开始注水1分钟,甲容器的水位上升a厘米,且比乙容器的水位低1厘米.其中a,k均为正整数,当甲、乙两个容器的水位都到达连通管子的位置时,停止注水.甲容器的水位有2次比乙容器的水位高1厘米,设注水时间为t分钟.

(1)求k的值(用含a的代数式表示).
(2)当甲容器的水位第一次比乙容器的水位高1厘米时,求t的值.
(3)当甲容器的水位第二次比乙容器的水位高1厘米时,求a,k,t的值.
相关试题

