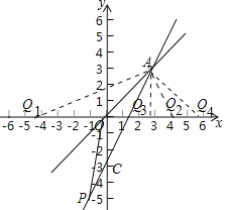
【题目】在平面直角坐标系中,直线l1的函数关系式为y=2x+b,直线l2过原点且与直线l1交于点P(-1,-5).
(1)试问(-1,-5)可以看作是怎样的二元一次方程组的解?
(2)设直线l1与直线y=x交于点A,求△APO的面积;
(3)在x轴上是否存在点Q,使得△AOQ是等腰三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
参考答案:
【答案】(1)(-1,-5)可以看成二元一次方程组![]() 的解;(2)S△AOP=6;(3)存在,点Q坐标为(-3
的解;(2)S△AOP=6;(3)存在,点Q坐标为(-3![]() ,0)或(3,0)或(3
,0)或(3,0)或(3![]() ,0)或(6,0).
,0)或(6,0).
【解析】
(1)求出直线![]() 与直线
与直线![]() 的解析式即可解决问题;
的解析式即可解决问题;
(2)利用方程组求出点A坐标,再求出直线![]() 与y轴的交点C的坐标,然后根据
与y轴的交点C的坐标,然后根据![]() 计算即可;
计算即可;
(3)根据等腰三角形的定义,分![]() 三种情形,然后利用两点之间的距离公式分别求解即可.
三种情形,然后利用两点之间的距离公式分别求解即可.
(1)∵点![]() 在直线
在直线![]() 上
上
![]() ,解得
,解得![]()
∴直线![]() 的解析式为
的解析式为![]()
设直线![]() 的解析式为
的解析式为![]()
则有![]() ,解得
,解得![]()
∴直线![]() 的解析式为
的解析式为![]()
故![]() 可以看成二元一次方程组
可以看成二元一次方程组![]() 的解;
的解;
(2)由![]() ,解得
,解得![]()
![]()
∵点![]() 在直线
在直线![]() 上,直线
上,直线![]() 交y轴于
交y轴于![]()
![]()
故![]() 的面积为6;
的面积为6;
(3)![]()
![]()
设点Q坐标为![]()
由等腰三角形的定义,分以下三种情况:
①当![]() 时,则
时,则![]() ,即
,即![]()
②当![]() 时,则
时,则![]()
解得![]() ,即
,即![]()
③当![]() 时,则
时,则![]()
解得![]() 或
或![]() (与点O重合,舍去),即
(与点O重合,舍去),即![]()
综上,满足条件的点Q坐标为![]() 或
或![]() 或
或![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2
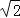 ,求正方形ADCE周长.
,求正方形ADCE周长. -
科目: 来源: 题型:
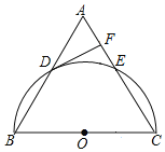
查看答案和解析>>【题目】如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若DF=3,EF=1,求弦EC的长.
-
科目: 来源: 题型:
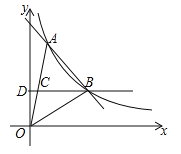
查看答案和解析>>【题目】(2017山东省菏泽市,第20题,7分)如图,一次函数y=kx+b与反比例函数
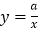 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)5x﹣6=3x+2;
(2)1﹣3(8﹣x)=﹣2(15﹣2x);
(3)
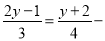 1;
1;(4)
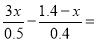 1.
1. -
科目: 来源: 题型:
查看答案和解析>>【题目】(2017广东省)如图,AB是⊙O的直径,AB=
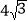 ,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.
,点E为线段OB上一点(不与O,B重合),作CE⊥OB,交⊙O于点C,垂足为点E,作直径CD,过点C的切线交DB的延长线于点P,AF⊥PC于点F,连接CB.(1)求证:CB是∠ECP的平分线;
(2)求证:CF=CE;
(3)当
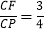 时,求劣弧
时,求劣弧 的长度(结果保留π)
的长度(结果保留π)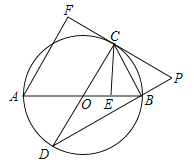
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一个半径为2cm的圆分成3个扇形,其圆心角的比1:2:3,求:
①各个扇形的圆心角的度数.
②其中最大一个扇形的面积.
相关试题

