【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,连接DE交AC于点F.

(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.
(3)在(2)的条件下,若AB=AC=2![]() ,求正方形ADCE周长.
,求正方形ADCE周长.
参考答案:
【答案】(1)见解析;(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,(3)8.
【解析】
试题分析:(1)根据等腰三角形的性质,可得∠CAD=![]() ∠BAC,根据等式的性质,可得∠CAD+∠CAE=
∠BAC,根据等式的性质,可得∠CAD+∠CAE=![]() (∠BAC+∠CAM)=90°,根据垂线的定义,可得∠ADC=∠CEA,根据矩形的判定,可得答案;
(∠BAC+∠CAM)=90°,根据垂线的定义,可得∠ADC=∠CEA,根据矩形的判定,可得答案;
(2)根据等腰直角三角形的性质,可得AD与CD的关系,根据正方形的判定,可得答案;
(3)根据勾股定理,可得AD的长,根据正方形周长公式,可得答案.
(1)证明:∵AB=AC,AD⊥BC,垂足为点D,
∴∠CAD=![]() ∠BAC.
∠BAC.
∵AN是△ABC外角∠CAM的平分线,
∴∠CAE=![]() ∠CAM.
∠CAM.
∵∠BAC与∠CAM是邻补角,
∴∠BAC+∠CAM=180°,
∴∠CAD+∠CAE=![]() (∠BAC+∠CAM)=90°.
(∠BAC+∠CAM)=90°.
∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形;
(2)∠BAC=90°且AB=AC时,四边形ADCE是一个正方形,
证明:∵∠BAC=90°且AB=AC,AD⊥BC,
∴∠CAD=![]() ∠BAC=45,∠ADC=90°,
∠BAC=45,∠ADC=90°,
∴∠ACD=∠CAD=45°,
∴AD=CD.
∵四边形ADCE为矩形,
∴四边形ADCE为正方形;
(3)解:由勾股定理,得
![]() =AB,AD=CD,
=AB,AD=CD,
即![]() AD=2
AD=2![]() ,
,
AD=2,
正方形ADCE周长4AD=4×2=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】3 120 000用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,三架飞机P,Q,R保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1),30秒后,飞机P飞到P′(4,3)位置,则飞机Q,R的位置Q′,R′分别为( )
A. Q′(2,3),R′(4,1) B. Q′(2,3),R′(2,1)
C. Q′(2,2),R′(4,1) D. Q′(3,3),R′(3,1)
-
科目: 来源: 题型:
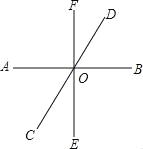
查看答案和解析>>【题目】如图,直线AB、CD、EF相交于点O.
(1)写出∠COE的邻补角;
(2)分别写出∠COE和∠BOE的对顶角;
(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列算式中,运算结果为负数的是( )
A. ﹣|﹣3| B. ﹣(﹣2)3 C. ﹣(﹣5) D. (﹣3)2
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲独做12天完成工作,乙工作效率比甲高20℅,则乙完成这项工作的天数为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的标价为200元,8折销售仍赚40元,则商品进价为( )元.
A.140 B.120 C.160 D.100
相关试题

