【题目】如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].
(1)若点D与点A重合,则这个操作过程为FZ[ , ];
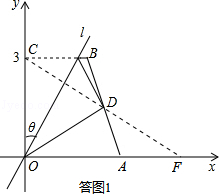
(2)若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
参考答案:
【答案】
(1)45°;3
(2)
解:如答图1所示,连接CD并延长,交x轴于点F.
在△BCD与△AFD中,
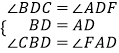
∴△BCD≌△AFD(ASA).
∴CD=FD,即点D为Rt△COF斜边CF的中点,
∴OD= ![]() CF=CD.
CF=CD.
又由折叠可知,OD=OC,
∴OD=OC=CD,
∴△OCD为等边三角形,∠COD=60°,
∴θ= ![]() ∠COD=30°
∠COD=30°
(3)
解:经过FZ[45°,a]操作,点B落在点E处,则点D落在x轴上,AB⊥直线l,
如答图2所示:
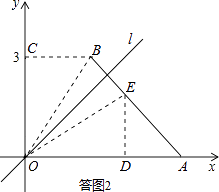
若点E在四边形0ABC的边AB上,
由折叠可知,OD=OC=3,DE=BC=2.
∵AB⊥直线l,θ=45°,
∴△ADE为等腰直角三角形,
∴AD=DE=2,
∴OA=OD+AD=3+2=5,
∴a=5;
由答图2可知,当0<a<5时,点E落在四边形0ABC的外部
(4)
解:满足条件的图形有两种,如答图3、答图4所示
FZ[30°,2+ ![]() ],FZ[60°,2+
],FZ[60°,2+ ![]() ].
].
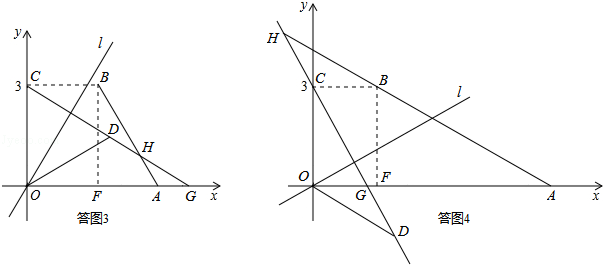
【解析】(1)若点D与点A重合,由折叠性质可知,OA=OC=3,θ= ![]() ∠AOC=45°,
∠AOC=45°,
∴FZ[45°,3].
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线
的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是【 】
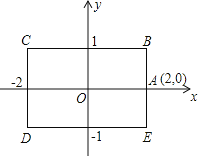
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD各顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).

(1)确定这个四边形的面积,你是怎样做的?
(2)如果把四边形ABCD各顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A关于y轴的对称点为点B,点B关于x轴的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出ΔABC,设AB与y轴的交点为D,求的值;
(2)若点A的坐标为(a,b)(ab≠0),判断ΔABC的形状.
-
科目: 来源: 题型:
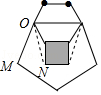
查看答案和解析>>【题目】如图,是一副形似“秋蝉”的图案,其实线部分是由正方形、正五边形和正六边形叠放在一起形成的,则图中∠MON的度数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知双曲线y=
 (k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,6),则△AOC的面积为 .
(k<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C.若点A的坐标为(﹣8,6),则△AOC的面积为 . 
相关试题

