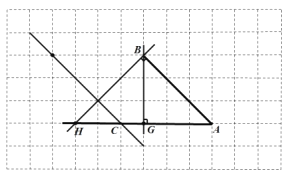
【题目】如图,由相同边长的小正方形组成的网格图形,A、B、C都在格点上,利用网格画图:(注:所画线条用黑色签字笔描黑)
(1)过点C画AB的平行线;
(2)过点B画AC的垂线,垂足为点G;过点B画AB的垂线,交AC的延长线于H.
(3)点B到AC的距离是线段 的长度,线段AB的长度是点 到直线
的距离.
(4)线段BG、AB的大小关系为:BG AB(填“>”、“<”或“=”),理由是 .

参考答案:
【答案】(1)如图 ;(2)如图 ;(3)BG、A、BH;
(4)<,直线外一点与直线上各点连接的所有线段中,垂线段最短;
【解析】(1)按要求作出AB的平行线即可;
(2)按要求作出AB、AC的垂线即可;
(3)根据点到直线的距离即可求解;
(4)根据垂线段最短即可得出答案.
解:(1)过点C画AB的平行线如图所示;
(2)过B画AC、AB的垂线如图所示;

(3)点B到AC的距离是线段BG 的长度,线段AB的长度是点A 到直线BH的距离.
(4)根据直线外一点与直线上各点连接的所有线段中,垂线段最短可知BG<AB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若点C为线段AB上一点,AB=12,AC=8,点D为直线AB上一点,M、N分别是AB、CD的中点,若MN=10,则线段AD的长为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是由一些棱长都为1的小正方体组合成的简单几何体.

(1)请画出这个几何体的三视图并用阴影表示出来;
(2)该几何体的表面积(含下底面)为 ;
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加 个小正方体.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,经过原点的抛物线y=﹣x2+2mx(m>0)与x轴的另一个交点为A.过点P(1,m)作直线PM⊥x轴于点M,交抛物线于点B.记点B关于抛物线对称轴的对称点为C(B、C不重合).连接CB,CP.

(1)当m=3时,求点A的坐标及BC的长;
(2)当m>1时,连接CA,问m为何值时CA⊥CP?
(3)过点P作PE⊥PC且PE=PC,问是否存在m,使得点E落在坐标轴上?若存在,求出所有满足要求的m的值,并定出相对应的点E坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形BCDE的各边分别平行于x轴或y轴,物体甲和物体乙分别由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2012次相遇地点的坐标是【 】
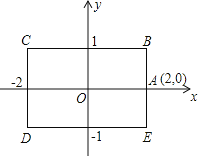
A.(2,0) B.(-1,1) C.(-2,1) D.(-1,-1)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD各顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).

(1)确定这个四边形的面积,你是怎样做的?
(2)如果把四边形ABCD各顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xOy中,已知点A(a,0)(a>0),B(2,3),C(0,3).过原点O作直线l,使它经过第一、三象限,直线l与y轴的正半轴所成角设为θ,将四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,我们把这个操作过程记为FZ[θ,a].

(1)若点D与点A重合,则这个操作过程为FZ[ , ];
(2)若点D恰为AB的中点(如图2),求θ;
(3)经过FZ[45°,a]操作,点B落在点E处,若点E在四边形0ABC的边AB上,求出a的值;若点E落在四边形0ABC的外部,直接写出a的取值范围;
(4)经过FZ[θ,a]操作后,作直线CD交x轴于点G,交直线AB于点H,使得△ODG与△GAH是一对相似的等腰三角形,直接写出FZ[θ,a].
相关试题

