搜索
【题目】如图，是一副形似“秋蝉”的图案，其实线部分是由正方形、正五边形和正六边形叠放在一起形成的，则图中∠MON的度数为 ．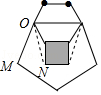 
参考答案：
【答案】33°
【解析】解：由正方形、正五边形和正六边形的性质得，∠AOM=108°，∠OBC=120°，∠NBC=90°， ∴∠AOB= 
120°=60°，∠MOB=108°﹣60°=48°，
∴∠OBN=360°﹣120°﹣90°=150°，
∴∠NOB= 
（180°﹣150°）=15°，
∴∠MON=33°，
所以答案是：33°．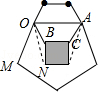
【考点精析】解答此题的关键在于理解多边形内角与外角的相关知识，掌握多边形的内角和定理：n边形的内角和等于（n-2）180°.多边形的外角和定理：任意多边形的外角和等于360°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD各顶点的坐标分别为(－2，8)，(－11，6)，(－14，0)，(0，0)．
(1)确定这个四边形的面积，你是怎样做的？
(2)如果把四边形ABCD各顶点纵坐标保持不变，横坐标增加2，所得的四边形面积又是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系xOy中，已知点A（a，0）（a＞0），B（2，3），C（0，3）．过原点O作直线l，使它经过第一、三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．
（1）若点D与点A重合，则这个操作过程为FZ[ ， ]；
（2）若点D恰为AB的中点（如图2），求θ；
（3）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形0ABC的边AB上，求出a的值；若点E落在四边形0ABC的外部，直接写出a的取值范围；
（4）经过FZ[θ，a]操作后，作直线CD交x轴于点G，交直线AB于点H，使得△ODG与△GAH是一对相似的等腰三角形，直接写出FZ[θ，a]． -
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系中,点A关于y轴的对称点为点B,点B关于x轴的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出ΔABC,设AB与y轴的交点为D,求的值;
(2)若点A的坐标为(a,b)(ab≠0),判断ΔABC的形状.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知双曲线y=
（k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣8，6），则△AOC的面积为 ． 
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读，再解决问题，例题：若m2+2mn+2n2﹣6n+9=0，求m和n的值.
解：∵m2+2mn+2n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0，n﹣3=0
∴n=3，m=﹣3
(1)若x2+2y2﹣2xy+4y+4=0，求xy的值
(2)已知△ABC的三边长a，b，c都是正整数，且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0，请问△ABC是怎样形状的三角形？
(3)根据以上的方法是说明代数式：x2+4x+y2﹣8y+21的值一定是一个正数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=12，AB=10，则AE的长为（ ）
A．16 B．15 C．14 D．13
相关试题
