搜索
【题目】如图，已知双曲线y= 
（k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣8，6），则△AOC的面积为 ． 
参考答案：
【答案】18
【解析】解：∵点D为线段OA的中点，且点A的坐标为（﹣8，6）， ∴点D的坐标为（﹣4，3）．
将点D（﹣4，3）代入到y= 
中得：
3= 
，解得：k=﹣12．
∴双曲线的解析式为y=﹣ 
．
令x=﹣8，则有y=﹣ 
= 
，
即点C的坐标为（﹣8， ）．
∵AB⊥BD，
∴点B（﹣8，0），AC=6﹣ = 
，OB=0﹣（﹣8）=8，
∴△AOC的面积S= 
ACOB= × ×8=18．
所以答案是：18．
【考点精析】通过灵活运用比例系数k的几何意义，掌握几何意义：表示反比例函数图像上的点向两坐标轴所作的垂线段与两坐标轴围成的矩形的面积即可以解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系xOy中，已知点A（a，0）（a＞0），B（2，3），C（0，3）．过原点O作直线l，使它经过第一、三象限，直线l与y轴的正半轴所成角设为θ，将四边形OABC的直角∠OCB沿直线l折叠，点C落在点D处，我们把这个操作过程记为FZ[θ，a]．
（1）若点D与点A重合，则这个操作过程为FZ[ ， ]；
（2）若点D恰为AB的中点（如图2），求θ；
（3）经过FZ[45°，a]操作，点B落在点E处，若点E在四边形0ABC的边AB上，求出a的值；若点E落在四边形0ABC的外部，直接写出a的取值范围；
（4）经过FZ[θ，a]操作后，作直线CD交x轴于点G，交直线AB于点H，使得△ODG与△GAH是一对相似的等腰三角形，直接写出FZ[θ，a]． -
科目： 来源： 题型：
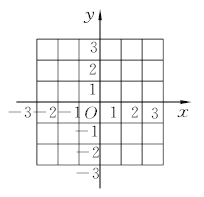
查看答案和解析>>【题目】在平面直角坐标系中,点A关于y轴的对称点为点B,点B关于x轴的对称点为点C.
(1)若点A的坐标为(1,2),请你在给出的坐标系中画出ΔABC,设AB与y轴的交点为D,求的值;
(2)若点A的坐标为(a,b)(ab≠0),判断ΔABC的形状.
-
科目： 来源： 题型：
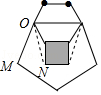
查看答案和解析>>【题目】如图，是一副形似“秋蝉”的图案，其实线部分是由正方形、正五边形和正六边形叠放在一起形成的，则图中∠MON的度数为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先阅读，再解决问题，例题：若m2+2mn+2n2﹣6n+9=0，求m和n的值.
解：∵m2+2mn+2n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0，n﹣3=0
∴n=3，m=﹣3
(1)若x2+2y2﹣2xy+4y+4=0，求xy的值
(2)已知△ABC的三边长a，b，c都是正整数，且满足a2+b2﹣6a﹣6b+18+|3﹣c|=0，请问△ABC是怎样形状的三角形？
(3)根据以上的方法是说明代数式：x2+4x+y2﹣8y+21的值一定是一个正数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平行四边形ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF=12，AB=10，则AE的长为（ ）
A．16 B．15 C．14 D．13
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AC⊥CB，垂足为C点，AC＝CB＝8cm，点Q是AC的中点，动点P由B点出发，沿射线BC方向匀速移动．点P的运动速度为2cm/s．设动点P运动的时间为ts．为方便说明，我们分别记三角形ABC面积为S，三角形PCQ的面积为S1，三角形PAQ的面积为S2，三角形ABP的面积为S3．
（1）S3＝ cm2（用含t的代数式表示）；
（2）当点P运动几秒，S1＝
S，说明理由；（3）请你探索是否存在某一时刻，使得S1＝S2＝S3？若存在，求出t值；若不存在，说明理由．
相关试题
