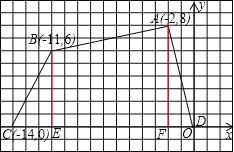
【题目】如图,四边形ABCD各顶点的坐标分别为(-2,8),(-11,6),(-14,0),(0,0).

(1)确定这个四边形的面积,你是怎样做的?
(2)如果把四边形ABCD各顶点纵坐标保持不变,横坐标增加2,所得的四边形面积又是多少?
参考答案:
【答案】(1) 80;(2)80
解:(1) (1)S四边形ABCD=14×8-![]() ×8×2-2×3-
×8×2-2×3-![]() ×2×9-
×2×9-![]() ×3×6=112-8-6-9-9=80 (2)各顶点纵坐标保持不变,横坐标增加2,即把四边形ABCD向右平移2个单位,所以形状、大小不发生改变,面积也不变,仍是80
×3×6=112-8-6-9-9=80 (2)各顶点纵坐标保持不变,横坐标增加2,即把四边形ABCD向右平移2个单位,所以形状、大小不发生改变,面积也不变,仍是80
【解析】试题分析:(1)过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,把四边形ABCD的面积分成两个三角形的面积与梯形的面积的和,然后列式求解即可;
(2)横坐标增加2,纵坐标不变,就是把四边形ABCD向右平移2个单位,根据平移的性质,四边形的面积不变.
试题解析:(1)如图,过点A作AF⊥x轴,过点B作BE⊥x轴,
则DF=2,CE=3,AF=8,BE=6,EF=-2-(-11)=9,
四边形ABCD的面积=S△ADF+S△BCE+S梯形ABEF,
=![]() ×2×8+
×2×8+![]() ×3×6+
×3×6+![]() ×(6+8)×9,
×(6+8)×9,
=8+9+63,
=80;
(2)四边形ABCD各个顶点的纵坐标保持不变,横坐标增加4,
就是把四边形ABCD向右平移4个单位,
所以,所得的四边形的面积不变,还是80.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A(﹣m,n),B(0,m),且m、n满足
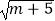 +(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处.
+(n﹣5)2=0,点C在y轴上,将△ABC沿y轴折叠,使点A落在点D处. 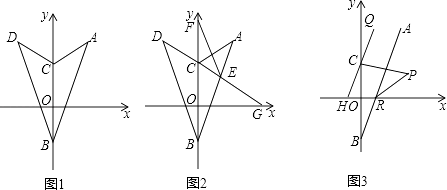
(1)写出D点坐标并求A、D两点间的距离;
(2)若EF平分∠AED,若∠ACF﹣∠AEF=20°,求∠EFB的度数;
(3)过点C作QH平行于AB交x轴于点H,点Q在HC的延长线上,AB交x轴于点R,CP、RP分别平分∠BCQ和∠ARX,当点C在y轴上运动时,∠CPR的度数是否发生变化?若不变,求其度数;若变化,求其变化范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,D(0,﹣3),M(4,﹣3),直角三角形ABC的边与x轴分别交于O、G两点,与直线DM分别交于E、F点.
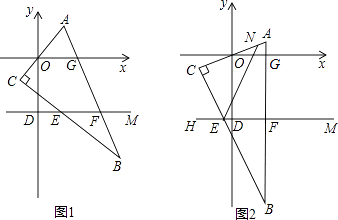
(1)将直角三角形ABC如图1位置摆放,请写出∠CEF与∠AOG之间的等量关系: .
(2)将直角三角形ABC如图2位置摆放,N为AC上一点,∠NED+∠CEF=180°,请写出∠NEF与∠AOG之间的等量关系,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
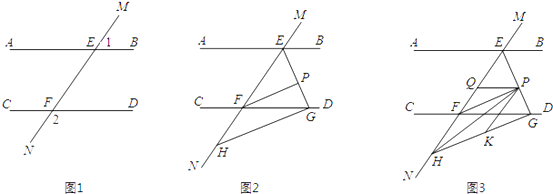
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】把70°15′化成度,则70°15′=_____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】
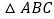 与
与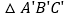 在平面直角坐标系中的位置如图.
在平面直角坐标系中的位置如图.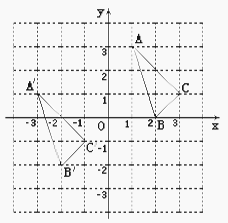
(1)分别写出下列各点的坐标:
 ________,
________, 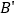 ________,
________, 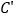 ________;
________; (2)说明
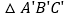 由
由 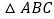 经过怎样的平移得到:________;
经过怎样的平移得到:________; (3)若点
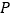 (
( 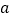 ,
,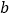 )是
)是 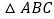 内部一点,则平移后
内部一点,则平移后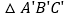 内的对应点
内的对应点 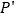 的坐标为________;
的坐标为________; (4)求
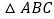 的面积.
的面积. -
科目: 来源: 题型:
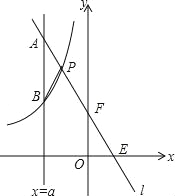
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象l与坐标轴分别交于点E、F,与双曲线y=
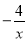 (x<0)交于点P(﹣1,n),且F是PE的中点.
(x<0)交于点P(﹣1,n),且F是PE的中点.(1)求直线l的解析式;
(2)若直线x=a与l交于点A,与双曲线交于点B(不同于A),问a为何值时,PA=PB?
相关试题

