【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD、DE、CE有怎样的等量关系?直接写出结果.

参考答案:
【答案】(1)△ADB≌△BEC,理由见解析;(2)CE+AD=DE,理由见解析;(3)CE﹣AD=DE,理由见解析;
【解析】
(1)求出∠ADB=∠ABC=∠BEC=90°,求出∠DAB=∠CBE,根据AAS推出△ADB≌△BEC即可;
(2)根据全等得出AD=BE,CE=DB,即可求出答案;
(3)证明过程和(1)(2)类似.
解:(1)△ADB≌△BEC,
理由是:∵AD⊥PQ,CE⊥PQ,
∴∠ADB=∠ABC=∠BEC=90°,
∴∠DAB+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠DAB=∠CBE,
在△ADB和△BEC中,
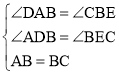 ,
,
∴△ADB≌△BEC(AAS);
(2)CE+AD=DE,
理由是:∵△ADB≌△BEC,
∴AD=BE,CE=DB,
∵DB+BE=DE,
∴CE+AD=DE;
(3)CE-AD=DE,
理由是:∵AD⊥PQ,CE⊥PQ,
∴∠ADB=∠ABC=∠BEC=90°,
∴∠DAB+∠ABD=90°,∠ABD+∠CBE=90°,
∴∠DAB=∠CBE,
在△ADB和△BEC中,
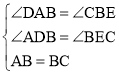 ,
,
∴△ADB≌△BEC(AAS),
∴AD=BE,CE=DB,
∵DB-BE=DE,
∴CE-AD=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
, ,
, 平分
平分 ,过点
,过点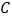 作
作 于点
于点 ,延长
,延长 ,
, 交于点
交于点 ,下列结论中:①
,下列结论中:① ;②
;② ;③
;③ ;④
;④ .正确的是( )
.正确的是( )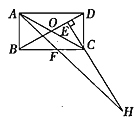
A.②③B.③④C.①②④D.②③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两队进行拔河比赛,裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是:石头胜剪子,剪子胜布,布胜石头,手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平,为什么?(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】将三角形纸片ABC沿DE折叠,其中AB=AC.
(1)如图①,当点C落在BC边上的点F处时,AB与DF是否平行?请说明理由;
(2)如图②,当点C落在四边形ABED内部的点G处时,探索∠B与∠1+∠2之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以顶点A为圆心,AD长为半径,在AB边上截取AE=AD,用尺规作图法作出∠BAD的角平分线AG,若AD=5,DE=6,则AG的长是_________________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型
A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
相关试题

