【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,
,![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,延长
,延长![]() ,
,![]() 交于点
交于点![]() ,下列结论中:①
,下列结论中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .正确的是( )
.正确的是( )
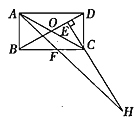
A.②③B.③④C.①②④D.②③④
参考答案:
【答案】D
【解析】
求出OA=OC=OD=OB,求出∠ADB=30°,求出∠ABO=60°,得出等边三角形AOB,求出AB=BO=AO=OD=OC=DC,推出BF=AB,求出∠H=∠CAH=15°,求出DE=EO,根据以上结论推出即可.
解:∵四边形ABCD是矩形,

∴∠BAD=90°,
∵AD=![]() ,AB=1,
,AB=1,
![]() ,
,
∴∠ADB=30°,
∴∠ABO=60°,
∵四边形ABCD是矩形,
∴AD∥BC,AC=BD,AC=2AO,BD=2BO,
∴AO=BO,
∴△ABO是等边三角形,
∴AB=BO,∠AOB=∠BAO=60°=∠COE,
∵AF平分∠BAD,
∴∠BAF=∠DAF=45°,
∵AD∥BC,
∴∠DAF=∠AFB,
∴∠BAF=∠AFB,
∴AB=BF,
∵AB=BO,
∴BF=BO,
∴②正确;
∵∠BAO=60°,∠BAF=45°,
∴∠CAH=15°,
∵CE⊥BD,
∴∠CEO=90°,
∵∠EOC=60°,
∴∠ECO=30°,
∴∠H=∠ECO-∠CAH=30°-15°=15°=∠CAH,
∴AC=CH,
∴③正确;
作HG⊥BC的延长线于点G,
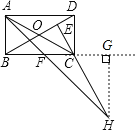
∴HG∥AB,∠BAF=∠FHG=45°,
∴∠CHG=∠FHG-∠H=45°-15°=30°,
∵AB=1,AD=![]() ,
,
∴BD=AC=CH=2,
∴![]() ,
,
∵∠BAF=∠FHG=45°,∠AFB=∠HFG,
∴△ABF∽△HGF,
![]()
即![]()
![]() ,
,
故①错误;
∵△AOB是等边三角形,
∴AO=OB=AB,
∵四边形ABCD是矩形,
∴OA=OC,OB=OD,AB=CD,
∴DC=OC=OD,△COD是等边三角形,
∵CE⊥BD,
![]() ,
,
即BE=3ED,∴④正确;
即正确的有②③④3个,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,∠B=40°,过点A的直线将这个三角形分成两个等腰三角形,则∠C的度数为______________.
-
科目: 来源: 题型:
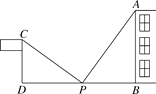
查看答案和解析>>【题目】如图,小强为了测量一幢高楼的高AB,在旗杆CD与楼之间选定一点P.测得旗杆顶C的视线PC与地面夹角∠DPC=36°,测得楼顶A的视线PA与地面夹角∠APB=54°,测得P到楼底距离PB与旗杆高度都为10米,测得旗杆与楼之间的距离DB=36米,据此小强计算出了楼高,求楼高AB是多少米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点E在BC上,CD⊥AB,EF⊥AB,垂足分别为D、F.
(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠ACB的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两队进行拔河比赛,裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是:石头胜剪子,剪子胜布,布胜石头,手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平,为什么?(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD、DE、CE有怎样的等量关系?直接写出结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将三角形纸片ABC沿DE折叠,其中AB=AC.
(1)如图①,当点C落在BC边上的点F处时,AB与DF是否平行?请说明理由;
(2)如图②,当点C落在四边形ABED内部的点G处时,探索∠B与∠1+∠2之间的数量关系,并说明理由.

相关试题

