【题目】如图,在平行四边形ABCD中,以顶点A为圆心,AD长为半径,在AB边上截取AE=AD,用尺规作图法作出∠BAD的角平分线AG,若AD=5,DE=6,则AG的长是_________________.

参考答案:
【答案】8
【解析】
首先证明线段AG与线段DE互相垂直平分,利用勾股定理求出AH即可解决问题;
解:分别以D和E作为圆心,以略长于EH的长度为半径作弧,交于点F,连接AF并延长,交CD于G,则AG即为∠BAD的角平分线,

设AG交BD于H,则AG垂直平分线线段DE(等腰三角形三线合一),
∴DH=EH=3,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴∠AGD=∠GAB,
∵∠DAG=∠GAB,
∴∠DAG=∠DGA,
∴DA=DG,
∵DE⊥AG,
∴AH=GH(等腰三角形三线合一),
在Rt△ADH中,AH= ![]() ,
,
∴AG=2AH=8,
故答案为8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两队进行拔河比赛,裁判员让两队队长用“石头、剪子、布”的手势方式选择场地位置.规则是:石头胜剪子,剪子胜布,布胜石头,手势相同再决胜负.请你说明裁判员的这种作法对甲、乙双方是否公平,为什么?(用树状图或列表法解答)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形ABC,AB=BC,直角顶点B在直线PQ上,且AD⊥PQ于D,CE⊥PQ于E.
(1)△ADB与△BEC全等吗?为什么?
(2)图1中,AD、DE、CE有怎样的等量关系?说明理由.
(3)将直线PQ绕点B旋转到如图2所示的位置,其他条件不变,那么AD、DE、CE有怎样的等量关系?直接写出结果.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将三角形纸片ABC沿DE折叠,其中AB=AC.
(1)如图①,当点C落在BC边上的点F处时,AB与DF是否平行?请说明理由;
(2)如图②,当点C落在四边形ABED内部的点G处时,探索∠B与∠1+∠2之间的数量关系,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场计划经销A、B两种新型节能台灯共50盏,这两种台灯的进价、售价如下表所示.
价格/类型
A型
B型
进价(元/盏)
40
65
售价(元/盏)
60
100
(1)若该商场购进这批台灯共用去2500元,问这两种台灯各购进多少盏?
(2)在每种台灯销售利润不变的情况下,若该商场销售这批台灯的总利润不少于1400元,问至少需购进B种台灯多少盏?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形
 中,点A的坐标是
中,点A的坐标是 ,点C的纵坐标是4,则B点的纵坐标是___________.
,点C的纵坐标是4,则B点的纵坐标是___________.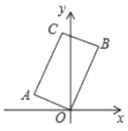
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在
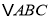 中,
中, ,点D在边
,点D在边 上,且
上,且 ,
,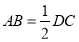 .则
.则 的度数为________°.
的度数为________°.
相关试题

