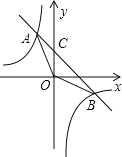
【题目】如图,一次函数y=kx+b的图象与反比例函数y=﹣![]() 的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:

(1)一次函数的表达式;
(2)△AOB的面积;
(3)根据图象,当x在什么范围内时,一次函数的值大于反比例函数的值?
参考答案:
【答案】(1)y=﹣x+2;(2)6;(3)x<﹣2和0<x<4.
【解析】
试题分析:(1)由反比例函数解析式可分别求得A、B两点的坐标,再利用待定系数法可求得一次函数表达式;
(2)设直线一次函数与y轴交于C点,可求得C点坐标,再利用三角形的面积公式计算即可;
(2)一次函数的值大于反比例函数的值时即一次函数的图象在反比例函数图象的上方,结合图象可求得x的范围.
解:
(1)反比例函数y=﹣![]() 的图象交于A、B两点,且A的横坐标和点B的纵坐标都是﹣2,
的图象交于A、B两点,且A的横坐标和点B的纵坐标都是﹣2,
∴A点的纵坐标为和B点的横坐标都为4,
∴A(﹣2,4),B(4,﹣2),
∵一次函数y=kx+b的图象过A、B两点,
∴把A、B两点坐标代入可得![]() ,解得
,解得![]() ,
,
∴一次函数表达式为y=﹣x+2;
(2)如图,设一次函数与y轴交于点C,则C点坐标为(0,2),
∴OC=2,
∴S△AOB=S△AOC+S△BOC=![]() OC2+
OC2+![]() OC4=6;
OC4=6;
(3)结合图象可知一次函数的图象在反比例函数图象的上方时,对应的x的取值范围为x<﹣2和0<x<4,
∴一次函数的值大于反比例函数的值时对应的x的取值范围为x<﹣2和0<x<4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A(﹣3,y1),B(3,y3),C(2,y2)二次函数y=x2+4x﹣5的图象上的三点,则y1、y2、y3的大小关系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.

(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,AB=6,BC=8,点E在线段AD上,把△ABE沿直线BE翻折,点A落在点A′,EA′的延长线交BC于点F,
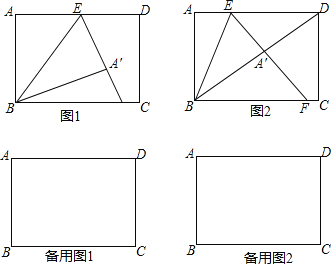
(1)如图(1),求证:FE=FB;
(2)当点E在边AD上移动时,点A′的位置也随之变化,
①当点A′恰好落在线段BD上时,如图(2),求AE的长;
②在运动变化过程中,设AE=x,CF=y,求y与x的函数关系式,试判断EF能否平分矩形ABCD的面积?若能,求出x的值;若不能,则说明理由;
(3)当点E在边AD上运动时,点D与点A′之间的距离也随之变化,请直接写出点D与点A′之间距离的变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车与乙车相遇后休息半小时,再按原速度继续前进到达B地;乙车从B地直接到达A地;两车到达各自目的地后即停止.如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)甲车的速度是 ,m= ;
(2)请分别写出两车在相遇前到B地的距离y(千米)与甲车出发时间x(小时)的函数关系式;
(3)当乙车行驶多少时间时,甲乙两车的距离是280千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AC、BD是一斜坡AB上的两幢楼房,斜坡AB的坡度是1:2
 ,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)
,从点A测得楼BD顶部D处的仰角60°,从点B测得楼AC顶部C处的仰角30°,楼BD自身高度BD比楼AC高12米,求楼AC和楼BD之间的水平距离?(结果保留根号)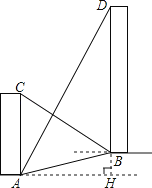
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有甲、乙两个构造完全相同的转盘均被分成A、B两个区域,甲转盘中A区域的圆心角是120°,乙转盘A区域的圆心角是90°,自由转动转盘,如果指针指向区域分界线则重新转动.
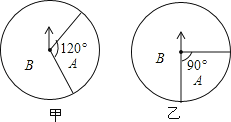
(1)转动甲转盘一次,则指针指向A区域的概率 ;
(2)自由转动两个转盘各一次,请用树状图或列表的方法,求出两个转盘同时指向B区域的概率?
相关试题

