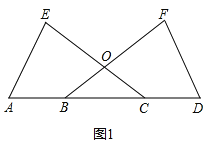
【题目】如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.

(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
参考答案:
【答案】(1)(2)证明见解析
【解析】
试题分析:(1)直接利用等腰三角形的性质结合全等三角形的判定与性质得出即可;
(2)利用翻折变换的性质得出∠DBG=∠DBF,再利用平行线的判定方法得出CE∥BG,进而求出四边形BGCE是平行四边形.
证明:(1)如图1,
∵OB=OC,
∴∠ACE=∠DBF,
在△ACE和△DBF中,
 ,
,
∴△ACE≌△DBF(AAS);
(2)如图2,
∵∠ACE=∠DBF,∠DBG=∠DBF,
∴∠ACE=∠DBG,
∴CE∥BG,
∵CE=BF,BG=BF,
∴CE=BG,
∴四边形BGCE是平行四边形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程x﹣2y+3=8,则整式x﹣2y的值为( )
A.5 B.10 C.12 D.15
-
科目: 来源: 题型:
查看答案和解析>>【题目】用“描点法”画二次函数y=ax2+bx+c(a≠0)的图象时,列出了如下表格:
x
…
1
2
3
4
…
y=ax2+bx+c
…
0
﹣1
0
3
…
那么该二次函数在x=0时,y=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若A(﹣3,y1),B(3,y3),C(2,y2)二次函数y=x2+4x﹣5的图象上的三点,则y1、y2、y3的大小关系是( )
A. y1<y2<y3 B. y2<y1<y3 C. y3<y1<y2 D. y1<y3<y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,AB=6,BC=8,点E在线段AD上,把△ABE沿直线BE翻折,点A落在点A′,EA′的延长线交BC于点F,
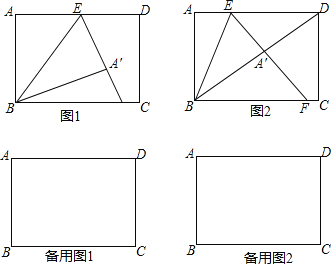
(1)如图(1),求证:FE=FB;
(2)当点E在边AD上移动时,点A′的位置也随之变化,
①当点A′恰好落在线段BD上时,如图(2),求AE的长;
②在运动变化过程中,设AE=x,CF=y,求y与x的函数关系式,试判断EF能否平分矩形ABCD的面积?若能,求出x的值;若不能,则说明理由;
(3)当点E在边AD上运动时,点D与点A′之间的距离也随之变化,请直接写出点D与点A′之间距离的变化范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图象与反比例函数y=﹣
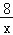 的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
的图象交于A、B两点,A的横坐标和点B的纵坐标都是﹣2.求:
(1)一次函数的表达式;
(2)△AOB的面积;
(3)根据图象,当x在什么范围内时,一次函数的值大于反比例函数的值?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两车分别从A、B两地同时出发相向而行,并以各自的速度匀速行驶,甲车与乙车相遇后休息半小时,再按原速度继续前进到达B地;乙车从B地直接到达A地;两车到达各自目的地后即停止.如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.

(1)甲车的速度是 ,m= ;
(2)请分别写出两车在相遇前到B地的距离y(千米)与甲车出发时间x(小时)的函数关系式;
(3)当乙车行驶多少时间时,甲乙两车的距离是280千米.
相关试题

