【题目】在![]() 中,
中,![]() .如图①,
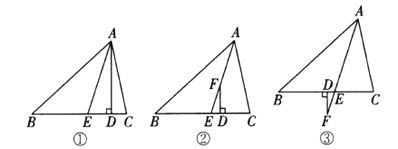
.如图①,![]() 于点
于点![]() ,
,![]() 平分
平分![]() ,则易知
,则易知![]() .
.
(1)如图②,![]() 平分
平分![]() ,
, ![]() 为
为![]() 上的一点,且
上的一点,且![]() 于点
于点![]() ,这时
,这时![]() 与
与![]() 、
、![]() 有何数量关系?请说明理由;
有何数量关系?请说明理由;
(2)如图③,![]() 平分
平分![]() ,
,![]() 为
为![]() 延长线上的一点,
延长线上的一点,![]() 于点
于点![]() ,请你写出这时
,请你写出这时![]() 与
与![]() 、
、![]() 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).
参考答案:
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B),外角的性质得出∠AEC=90°+
(∠C+∠B),外角的性质得出∠AEC=90°+![]() (∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(2)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B), 外角的性质得出∠DEF=90°+
(∠C+∠B), 外角的性质得出∠DEF=90°+![]() (∠B-∠C), 在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C), 在△EFD中,由三角形内角和定理可得∠EFD;
试题解析:
∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() =90°-
=90°-![]() (∠C+∠B),
(∠C+∠B),
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°-![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C)
(∠B-∠C)
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).
(2)∠EFD=![]() (∠C-∠B),理由如下:
(∠C-∠B),理由如下:
∵AE平分∠BAC,
∴∠BAE=![]() .
.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+![]() =90°+
=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C),
(∠B-∠C),
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)

-
科目: 来源: 题型:
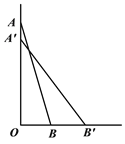
查看答案和解析>>【题目】已知:∠MON=80°,OE平分∠MON,点A、B、C分别是射线OM、OE、ON上的动点(A、B、C不与点O 重合),连接AC交射线OE于点D.设∠OAC=x°.
(1)如图1,若AB∥ON,则:①∠ABO的度数是 ;
②如图2,当∠BAD=∠ABD时,试求x的值(要说明理由);
(2)如图3,若AB⊥OM,则是否存在这样的X的值,使得△ADB中有两个相等的角?若存在,直接写出x的值;若不存在,说明理由.(自己画图)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架2.5米长的梯子斜立在竖直的墙上,此时梯足B距底端O为0.7米。(1)求OA的长度。(2)如果梯子顶端下滑0.4米,则梯子将滑出多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一块直角三角形的绿地,量得两直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
-
科目: 来源: 题型:
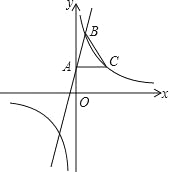
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=
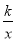 (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=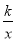 (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.(1)求反比例函数的表达式.
(2)求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一块长方形菜地的面积是150 m2,如果它的长减少5 m,那么菜地就变成正方形,若设原菜地的长为x m,则可列方程为___________________________________;
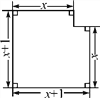
(2)已知如图所示的图形的面积为24,根据图中的条件,可列方程为__________________.
相关试题

