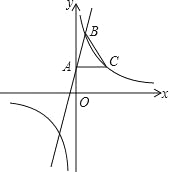
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.
参考答案:
【答案】(1)y=![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)先由一次函数y=3x+2的图象过点B,且点B的横坐标为1,将x=1代入y=3x+2,求出y的值,得到点B的坐标,再将B点坐标代入y=![]() ,利用待定系数法即可求出反比例函数的表达式;
,利用待定系数法即可求出反比例函数的表达式;
(2)先由一次函数y=3x+2的图象与y轴交于点A,求出点A的坐标为(0,2),再将y=2代入y=![]() ,求出x的值,那么AC=
,求出x的值,那么AC=![]() .过B作BD⊥AC于D,则BD=yB-yC=5-2=3,然后根据S△ABC=
.过B作BD⊥AC于D,则BD=yB-yC=5-2=3,然后根据S△ABC=![]() ACBD,将数值代入计算即可求解.
ACBD,将数值代入计算即可求解.
试题解析:(1)∵一次函数y=3x+2的图象过点B,且点B的横坐标为1,
∴y=3×1+2=5,
∴点B的坐标为(1,5).
∵点B在反比例函数y=![]() 的图象上,
的图象上,
∴k=1×5=5,
∴反比例函数的表达式为y=![]() ;
;
(2)∵一次函数y=3x+2的图象与y轴交于点A,
∴当x=0时,y=2,
∴点A的坐标为(0,2),
∵AC⊥y轴,
∴点C的纵坐标与点A的纵坐标相同,是2,
∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴当y=2时,2=![]() ,解得x=
,解得x=![]() ,
,
∴AC=![]() .
.
过B作BD⊥AC于D,则BD=yB-yC=5-2=3,
∴S△ABC=![]() ACBD=
ACBD=![]() ×
×![]() ×3=
×3=![]() .
.
-
科目: 来源: 题型:
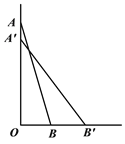
查看答案和解析>>【题目】如图,一架2.5米长的梯子斜立在竖直的墙上,此时梯足B距底端O为0.7米。(1)求OA的长度。(2)如果梯子顶端下滑0.4米,则梯子将滑出多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在
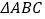 中,
中, .如图①,
.如图①,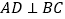 于点
于点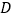 ,
,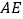 平分
平分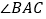 ,则易知
,则易知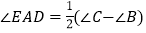 .
.(1)如图②,
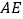 平分
平分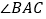 ,
, 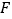 为
为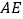 上的一点,且
上的一点,且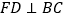 于点
于点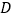 ,这时
,这时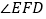 与
与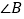 、
、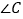 有何数量关系?请说明理由;
有何数量关系?请说明理由;(2)如图③,
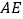 平分
平分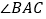 ,
,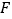 为
为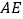 延长线上的一点,
延长线上的一点,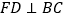 于点
于点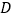 ,请你写出这时
,请你写出这时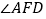 与
与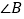 、
、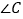 之间的数量关系(只写结论,不必说明理由).
之间的数量关系(只写结论,不必说明理由).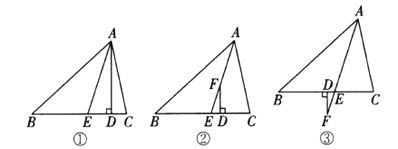
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一块直角三角形的绿地,量得两直角边长分别为6 m,8 m,现在要将绿地扩充成等腰三角形,且扩充部分是以8 m为直角边的直角三角形,求扩充后等腰三角形绿地的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)一块长方形菜地的面积是150 m2,如果它的长减少5 m,那么菜地就变成正方形,若设原菜地的长为x m,则可列方程为___________________________________;
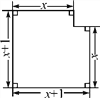
(2)已知如图所示的图形的面积为24,根据图中的条件,可列方程为__________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名射击运动员在某次训练中各射击10发子弹,成绩如下表:
甲
8
9
7
9
8
6
7
8
10
8
乙
6
7
9
7
9
10
8
7
7
10
且
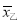 =8,
=8,  =1.8.根据上述信息完成下列问题:
=1.8.根据上述信息完成下列问题:(1)将甲运动员的折线统计图补充完整.
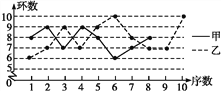
(2)求乙运动员射击训练成绩的众数和中位数.
(3)求甲运动员射击成绩的平均数和方差,并判断甲、乙两人本次射击成绩的稳定性.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【新知理解】
如图①,若点
 、
、 在直线l同侧,在直线l上找一点
在直线l同侧,在直线l上找一点 ,使
,使 的值最小.
的值最小.作法:作点
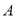 关于直线l的对称点
关于直线l的对称点 ,连接
,连接 交直线l于点
交直线l于点 ,则点
,则点 即为所求.
即为所求.【解决问题】
如图②,
 是边长为6cm的等边三角形
是边长为6cm的等边三角形 的中线,点
的中线,点 、
、 分别在
分别在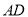 、
、 上,则
上,则 的最小值为 cm;
的最小值为 cm;【拓展研究】
如图③,在四边形
 的对角线
的对角线 上找一点
上找一点 ,使
,使 .(保留作图痕迹,并对作图方法进行说明)
.(保留作图痕迹,并对作图方法进行说明)
相关试题

