【题目】综合与实践:
如图,二次函数y=﹣![]() x2+
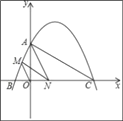
x2+![]() x+4的图象与x轴交于点B,点C(点B在点C的左边),与y轴交于点A,连接AC,AB.
x+4的图象与x轴交于点B,点C(点B在点C的左边),与y轴交于点A,连接AC,AB.
(1)求证:AO2=BOCO;
(2)若点N在线段BC上运动(不与点B,C重合),过点N作MN∥AC,交AB于点M,求当△AMN的面积取得最大值时,直线AN的表达式.
(3)连接OM,在(2)的结论下,试判断OM与AN的数量关系,并证明你的结论.
参考答案:
【答案】(1)证明见解析; (2)y=﹣![]() x+4;(3)OM2=AN.
x+4;(3)OM2=AN.
【解析】试题分析:(1)由分别令![]() 求得
求得![]() 的坐标,即可证明.
的坐标,即可证明.
(2)设点![]() 则
则![]() 由NM∥AC,可求得
由NM∥AC,可求得![]() 可用
可用![]() 表示出
表示出![]() 的面积,则可用
的面积,则可用![]() 表示出
表示出![]() 的面积,再利用二次函数的性质可求得其面积最大时
的面积,再利用二次函数的性质可求得其面积最大时![]() 的值,即可求得N点的坐标;进而用待定系数法求得直线AN的表达式.
的值,即可求得N点的坐标;进而用待定系数法求得直线AN的表达式.
(3)由N点坐标可求得M点为AB的中点,由直角三角形的性质可得![]()
在![]() 和
和![]() 中,可分别求得AB和
中,可分别求得AB和![]() 的长,可求得
的长,可求得![]() 的长度,从而可得到OM和
的长度,从而可得到OM和![]() 的数量关系.
的数量关系.
试题解析:(1)当![]() 时,
时, ![]() 整理得:
整理得: ![]() 解得:
解得: ![]()
∴![]()
令![]() 得:
得: ![]()
∴![]()
∴![]()
∴![]()
(2)设点![]() 则
则![]()
∵MN∥AC,
![]()
∵![]()
![]()
![]()
![]()
![]()
∴当![]() 时,即
时,即![]()
![]() 的面积最大.
的面积最大.
设直线AN的表达式为![]()
将点A和N的坐标代入得: ![]() 解得
解得 .
.
∴直线AN的表达式为![]()
(3)![]()
![]()
![]()
![]()
∴N为线段![]() 的中点.
的中点.
∵MN∥AC,
∴M为AB的中点,
∴![]()
∵![]()
∴![]()
∵![]()
![]() 即OM与AN的数量关系是
即OM与AN的数量关系是![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕
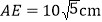 ,且
,且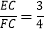 ,那么该矩形的周长为______cm.
,那么该矩形的周长为______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
问题情境:
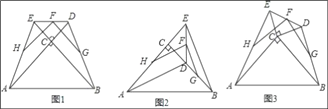
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=mx+n与反比例函数y=
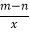 ,其中mn<0,m、n均为常数,它们在同一坐标系中的图象可以是( )
,其中mn<0,m、n均为常数,它们在同一坐标系中的图象可以是( )A.
 B.
B. 
C.
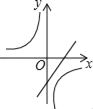 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),在三角形
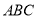 中,
中,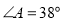 ,
,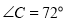 ,
,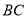 边绕点
边绕点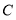 按逆时针方向旋转一周回到原来的位置(即旋转角
按逆时针方向旋转一周回到原来的位置(即旋转角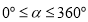 ),在旋转过程中(图2),当
),在旋转过程中(图2),当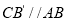 时,旋转角为________度;当
时,旋转角为________度;当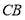 所在直线垂直于
所在直线垂直于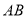 时,旋转角为__________度.
时,旋转角为__________度.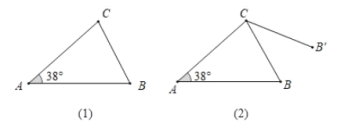
相关试题

