【题目】综合与探究
问题情境:
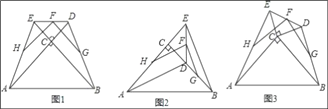
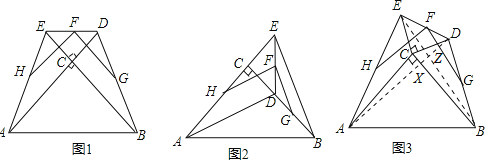
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
参考答案:
【答案】(1)FG=FH,FG⊥FH;(2)(1)中结论成立,证明见解析;
(3)(1)中的结论成立,结论是FH=FG,FH⊥FG.理由见解析.
【解析】试题分析:(1)证BE=AD,根据三角形的中位线推出FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE, 即可推出答案;
BE,FG∥BE, 即可推出答案;
(2)证△ACD≌△BCE,推出AD=BE,根据三角形的中位线定理即可推出答案;
(3)连接AD,BE,根据全等推出AD=BE,根据三角形的中位线定理即可推出答案.
试题解析:(1)∵CE=CD,AC=BC, ![]()
∴BE=AD,
∵F是DE的中点,H是AE的中点,G是BD的中点,
∴FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE,
BE,FG∥BE,
∴FH=FG,
∵AD⊥BE,
∴FH⊥FG,
故答案为:相等,垂直。
(2)答:成立,
证明:∵CE=CD, ![]() AC=BC,
AC=BC,
∴△ACD≌△BCE,
∴AD=BE,
由(1)知:FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE,
BE,FG∥BE,
∴FH=FG,FH⊥FG,
∴(1)中的猜想还成立.
(3)答:成立,结论是FH=FG,FH⊥FG.
连接AD,BE,两线交于Z,AD交BC于X,
同(1)可证
∴FH=![]() AD,FH∥AD,FG=
AD,FH∥AD,FG=![]() BE,FG∥BE,
BE,FG∥BE,
∵三角形ECD、ACB是等腰直角三角形,
∴CE=CD,AC=BC, ![]()
∴∠ACD=∠BCE,
在△ACD和△BCE中
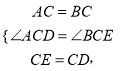
∴△ACD≌△BCE,
∴AD=BE,∠EBC=∠DAC,
∵![]() ∠CXA=∠DXB,
∠CXA=∠DXB,
∴![]()
∴![]() 即AD⊥BE,
即AD⊥BE,
∵FH∥AD,FG∥BE,
∴FH⊥FG,
即FH=FG,FH⊥FG,
结论是FH=FG,FH⊥FG
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小明想利用太阳光测量楼高,发现对面墙上有这栋楼的影子,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠且高度恰好相同.此时测得墙上影子高
 ,
, ,
, (点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.
(点A、E、C在同一直线上).已知小明身高EF是1.6m,则楼高AB为______m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线
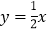 与反比例函数
与反比例函数 (
( )图像交于点A,将直线向右平移4个单位,交反比例函数
)图像交于点A,将直线向右平移4个单位,交反比例函数 (
( )图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.
)图像于点B,交y轴于点C,连结AB、AC,则△ABC的面积为_______.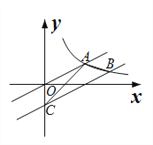
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕
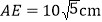 ,且
,且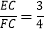 ,那么该矩形的周长为______cm.
,那么该矩形的周长为______cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,AB=AC,∠BAC=120°,AC的垂直平分线EF交AC于点E,交BC于点F.试探索BF与CF的数量关系,写出你的结论并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与实践:
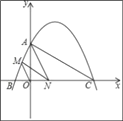
如图,二次函数y=﹣
 x2+
x2+ x+4的图象与x轴交于点B,点C(点B在点C的左边),与y轴交于点A,连接AC,AB.
x+4的图象与x轴交于点B,点C(点B在点C的左边),与y轴交于点A,连接AC,AB.(1)求证:AO2=BOCO;
(2)若点N在线段BC上运动(不与点B,C重合),过点N作MN∥AC,交AB于点M,求当△AMN的面积取得最大值时,直线AN的表达式.
(3)连接OM,在(2)的结论下,试判断OM与AN的数量关系,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状并说明理由.

相关试题

