【题目】如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,则AC长为( )

A. 2 B. 3 C. 4 D. 以上都不对
参考答案:
【答案】A
【解析】
根据线段垂直平分线上的点到两端点的距离相等可得AE=BE,再根据等边对等角可得∠BAE=∠B,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AEC=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得AC=![]() AE.
AE.
解:∵DE垂直平分AB交BC于点E,
∴AE=BE=4,
由AE=BE,可知∠B=∠EAB=15o,∠AEC是△ABE的外角,
∴∠AEC=∠B+∠EAB=30°,
∵∠C=90°,在Rt△AEC中,∠C=90°,∠AEC=30o,AE=4,
∴AC=![]() .
.
故选择A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是矩形ABCD的边CB的中点,AF⊥DE于点F,AB=3,AD=4.求点A到直线DE的距离.
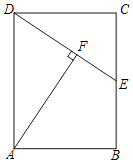
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面的文字,解答问题.
大家知道
 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用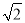 -1来表示
-1来表示 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为
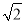 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.请解答:已知:10+
 =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )

A. 10 B. 8 C. 6 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边三角形ABC的边长为4,AD是BC边上的中线,F是AD边上的动点,E是AC边上一点.若AE=2,当EF+CF取得最小值时,∠ECF的度数为( )

A. 20° B. 25° C. 30° D. 45°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长均为1,△A1B1C1和△A2B2C2的顶点都在方格纸的格点上.

(1)求△A1B1C1和△A2B2C2的面积比.
(2)点A1、D、E、F、G、H是△A1B1C1边上的6个格点,请在这6个格点中选取3个点作为三角形的顶点,使构成的三角形与△A2B2C2相似(要求写出2个符合条件的三角形,并分别在图1和图2中将相应三角形涂黑,不必说明理由).
相关试题

