【题目】阅读下面的文字,解答问题.
大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部地写出来,于是小明用
的小数部分我们不可能全部地写出来,于是小明用![]() -1来表示
-1来表示![]() 的小数部分,你同意小明的表示方法吗?
的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为![]() 的整数部分是1,将这个数减去其整数部分,差就是小数部分.
的整数部分是1,将这个数减去其整数部分,差就是小数部分.
请解答:已知:10+![]() =x+y,其中x是整数,且0<y<1,求x-y的相反数.
=x+y,其中x是整数,且0<y<1,求x-y的相反数.
参考答案:
【答案】x="11," y=![]() -1, x-y的相反数
-1, x-y的相反数![]() -12
-12
【解析】本题主要考查了无理数的公式能力,解题关键是估算无理数的整数部分和小数部分. 根据题意的方法,估计![]() 的大小,易得10+
的大小,易得10+![]() 的范围,进而可得xy的值;再由相反数的求法,易得答案.
的范围,进而可得xy的值;再由相反数的求法,易得答案.
解:∵1<![]() <2,
<2,
∴1+10<10+![]() <2+10,
<2+10,
∴11<10+![]() <12,
<12,
∴x=11,
y=10+![]() -11=
-11=![]() -1,
-1,
x-y=11-(![]() -1)=12-
-1)=12-![]() ,
,
∴x-y的相反数![]() -12.
-12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠DAB=∠ABC=90°,AB=BC,E是AB的中点,CE⊥BD.

(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把下列各数填入相应的大括号内.
3
 ,-
,-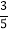 ,
,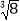 ,0.5,2π,3.14159265,-
,0.5,2π,3.14159265,- ,1.103030030003…(相
,1.103030030003…(相邻两个3之间依次多1个0).
(1) 有理数集合:{ };
(2) 无理数集合:{ };
(3) 实数集合:{ };
(4) 负实数集合:{ }.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E是矩形ABCD的边CB的中点,AF⊥DE于点F,AB=3,AD=4.求点A到直线DE的距离.
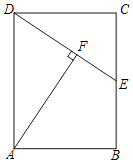
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点D是边AB的四等分点,DE∥AC,DF∥BC,AC=8,BC=12,求四边形DECF的周长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,∠B=15°,DE垂直平分AB交BC于点E,BE=4,则AC长为( )

A. 2 B. 3 C. 4 D. 以上都不对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知S△ABC=12,AD平分∠BAC,且AD⊥BD于点D,则S△ADC的值是( )

A. 10 B. 8 C. 6 D. 4
相关试题

