【题目】如果二次函数的二次项系数为1,那么此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标;
(2)探究下列问题:
①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度,求得到的图象对应的函数的特征数;
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
参考答案:
【答案】(1) (1,0);(2) ① [2,-3],②见解析
【解析】试题分析:首先根据函数的特征数可以确定函数表达式为y=x2-2x+1=(x-1)2,所以可得出顶点坐标为:(1,0);先根据函数的特征数写出函数的表达式,将表达式写成顶点式,然后再平移,平移时规律为左加右减,上加下减。求出平移后的函数表达式是顶点式,将顶点式化成y=x2+px+q的形式,即可求得特征数;如果已知两个函数的特征数,要想知道两个函数怎么平移得到的,需先将两个函数都转化成顶点式,再根据两个函数顶点式判断平移方法。
解:(1)由题意,得y=x2-2x+1=(x-1)2.
∴特征数为[-2,1]的函数图象的顶点坐标为(1,0).
(2)①特征数为[4,-1]的函数表达式为y=x2+4x-1
即y=(x+2)2-5.
∵函数图象先向右平移1个单位长度,再向上平移1个单位长度,
∴y=(x+2-1)2-5+1,即y=x2+2x-3.
∴特征数为[2,-3].
②特征数为[2,3]的函数表达式为y=x2+2x+3,即y=(x+1)2+2,
特征数为[3,4]的函数表达式为y=x2+3x+4,即
y=(x+![]() )2+
)2+![]() ,
,
∴所求平移为:先向左平移![]() 个单位长度,再向下平移
个单位长度,再向下平移![]() 个单位长度(或先向下平移
个单位长度(或先向下平移![]() 个单位长度,再向左平移
个单位长度,再向左平移![]() 个单位长度).
个单位长度).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,H是△ABC的高AD,BE的交点,且DH=DC,则下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD中正确的有( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
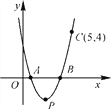
查看答案和解析>>【题目】如图,抛物线y=ax2-5ax+4a与x轴相交于点A,B,且过点C(5,4).
(1)求a的值和该抛物线顶点P的坐标;
(2)请你设计一种平移的方法,使平移后抛物线的顶点落在第二象限,并写出平移后抛物线的表达式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以下说法合理的是( )
A. 小明做了3次掷图钉的实验,发现2次钉尖朝上,由此他说钉尖朝上的概率是
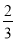
B. 某彩票的中奖概率是5%,那么买100张彩票一定有5张中奖
C. 某射击运动员射击一次只有两种可能的结果:中靶与不中靶,所以他击中靶的概率是
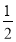
D. 小明做了3次掷均匀硬币的实验,其中有一次正面朝上,2次正面朝下,他认为再掷一次,正面朝上的概率还是
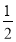
-
科目: 来源: 题型:
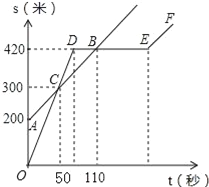
查看答案和解析>>【题目】某中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动朱老师先跑,当小明出发时,朱老师已经距起点200米了,他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).根据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是 ,因变量是 ;
(2)朱老师的速度为 米/秒;小明的速度为 米/秒;
(3)小明与朱老师相遇 次,相遇时距起点的距离分别为 米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 和
和 中,
中, ,
, ,
, ,且顶点D落在
,且顶点D落在 的内部(包含边上),连结
的内部(包含边上),连结 .当
.当 是以
是以 为腰的等腰直角三角形,则
为腰的等腰直角三角形,则 的面积为_____.
的面积为_____.
-
科目: 来源: 题型:
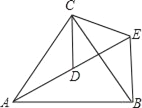
查看答案和解析>>【题目】如图,△ACB和△ECD都是等边三角形,点A、D、E在同一直线上,连接BE.
(1)求证:AD=BE;
(2)求∠AEB的度数.
相关试题

