【题目】阅读下列材料: 如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
(1)填空: ①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为 .
为半径的圆的方程为 .
(2)根据以上材料解决下列问题: 如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= ![]() .
.
①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
参考答案:
【答案】
(1)(x﹣3)2+y2=1;(x+1)2+(y+2)2=3
(2)解:①证明:∵BD⊥OC,
∴CD=OD,
∴BE垂直平分OC,
∴EO=EC,
∴∠EOC=∠ECO,
∵BO=BC,
∴∠BOC=∠BCO,
∴∠EOC+∠BOC=∠ECO+∠BCO,
∴∠BOE=∠BCE=90°,
∴BC⊥CE,
∴EC是⊙B的切线;
②存在.
∵∠BOE=∠BCE=90°,
∴点C和点O偶在以BE为直径的圆上,
∴当P点为BE的中点时,满足PB=PC=PE=PO,
∵B点坐标为(﹣6,0),
∴OB=6,
∵∠AOC+∠DOE=90°,∠DOE+∠BEO=90°,
∴∠BEO=∠AOC,
∴sin∠BEO=sin∠AOC= ![]() ,
,
在Rt△BOE中,sin∠BEO= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴BE=10,
∴OE= ![]() =8,
=8,
∴E点坐标为(0,8),
∴线段AB的中点P的坐标为(﹣3,4),PB=5,
∴以P(﹣3,4)为圆心,以5为半径的⊙P的方程为(x+3)2+(y﹣4)2=25.

【解析】(1)解:①以A(3,0)为圆心,1为半径的圆的方程为(x﹣3)2+y2=1; ②以B(﹣1,﹣2)为圆心, ![]() 为半径的圆的方程为(x+1)2+(y+2)2=3;
为半径的圆的方程为(x+1)2+(y+2)2=3;
故答案为(x﹣3)2+y2=1;(x+1)2+(y+2)2=3;
(1)根据阅读材料中的定义求解;(2)①根据垂径定理由BD⊥OC得到CD=OD,则BE垂直平分OC,再根据线段垂直平分线的性质得EO=EC,则∠EOC=∠ECO,加上∠BOC=∠BCO,易得∠BOE=∠BCE=90°,然后根据切线的判定定理得到EC是⊙B的切线;②由∠BOE=∠BCE=90°,根据圆周角定理得点C和点O偶在以BE为直径的圆上,即当P点为BE的中点时,满足PB=PC=PE=PO,利用同角的余角相等得∠BOE=∠AOC,则sin∠BOE=sin∠AOC= ![]() ,在Rt△BOE中,利用正弦的定义计算出BE=10,利用勾股定理计算出OE=8,则E点坐标为(0,8),于是得到线段AB的中点P的坐标为(﹣3,4),PB=5,然后写出以P(﹣3,4)为圆心,以5为半径的⊙P的方程.
,在Rt△BOE中,利用正弦的定义计算出BE=10,利用勾股定理计算出OE=8,则E点坐标为(0,8),于是得到线段AB的中点P的坐标为(﹣3,4),PB=5,然后写出以P(﹣3,4)为圆心,以5为半径的⊙P的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A(
 ,1)在反比例函数y=
,1)在反比例函数y=  的图象上.
的图象上.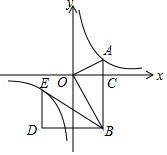
(1)求k的值;
(2)若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】请从以下两个小题中任选一个作答,若多选,则按所选的第一小题计分.
①若单项式﹣xmyn+4 与 5x2y 是同类项,则 nm 的值为____.
②实施西部大开发战略是党中央的重大决策,我国国土面积约为960 万平方千米,而我国西部地区的面积占我国国土面积的
 ,用科学记数法表示我国西部地区的面积约为_____平方千米.
,用科学记数法表示我国西部地区的面积约为_____平方千米. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD相交于点O,OA平分∠EOC.

(1)若∠EOC=70°,求∠BOD的度数;
(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m),且与y轴、直线x=2分别交于点D、E.

(1)求m的值及该抛物线对应的函数关系式;
(2)判断直线BE与抛物线交点的个数;
(3)求证:CD垂直平分BE;
(4)若P是该抛物线上的一个动点,是否存在这样的点P,使得△PBE是等腰直角三角形,且∠PEB=90°?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).

(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.
相关试题

